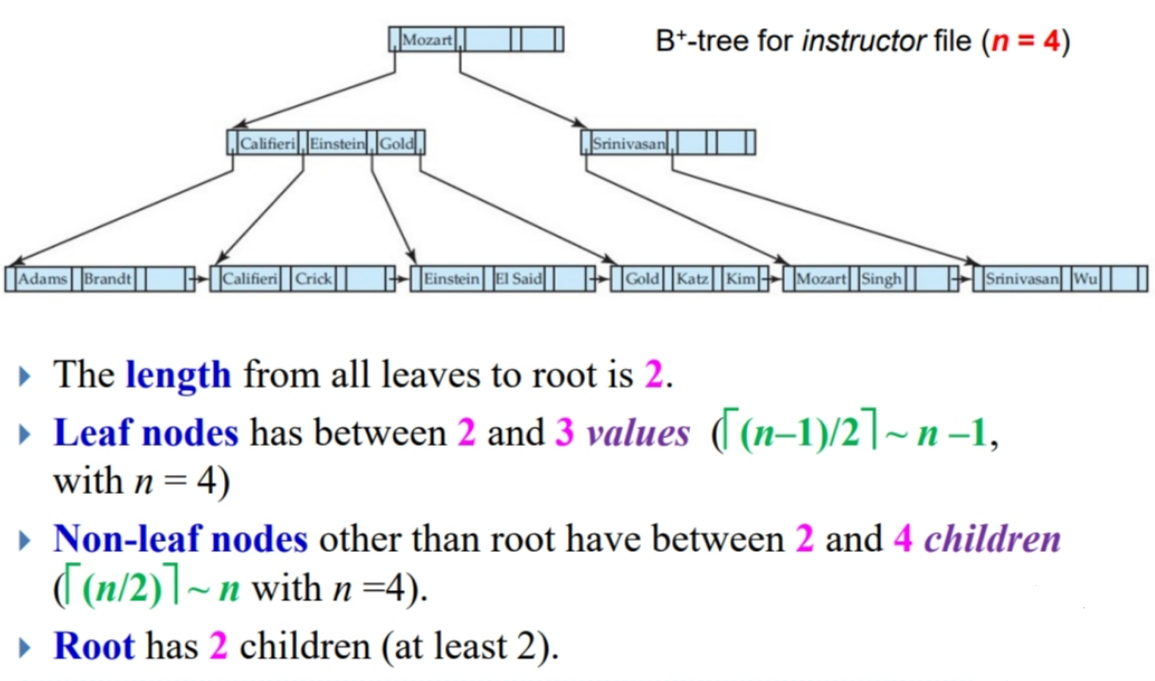
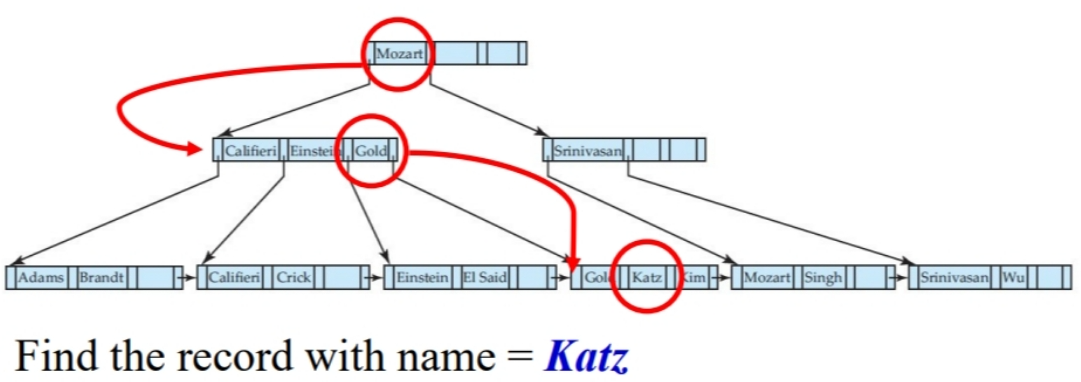
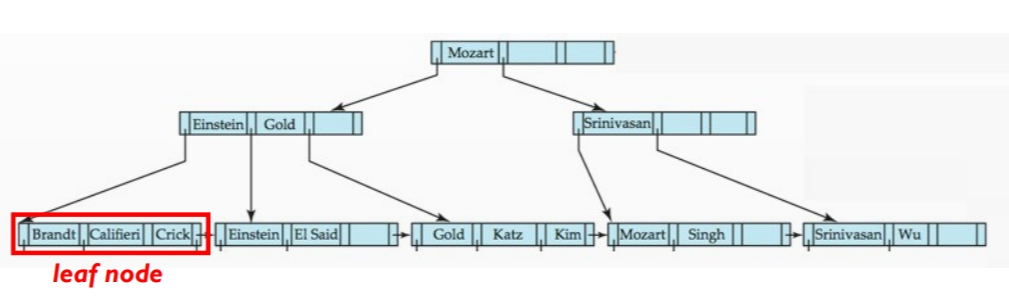
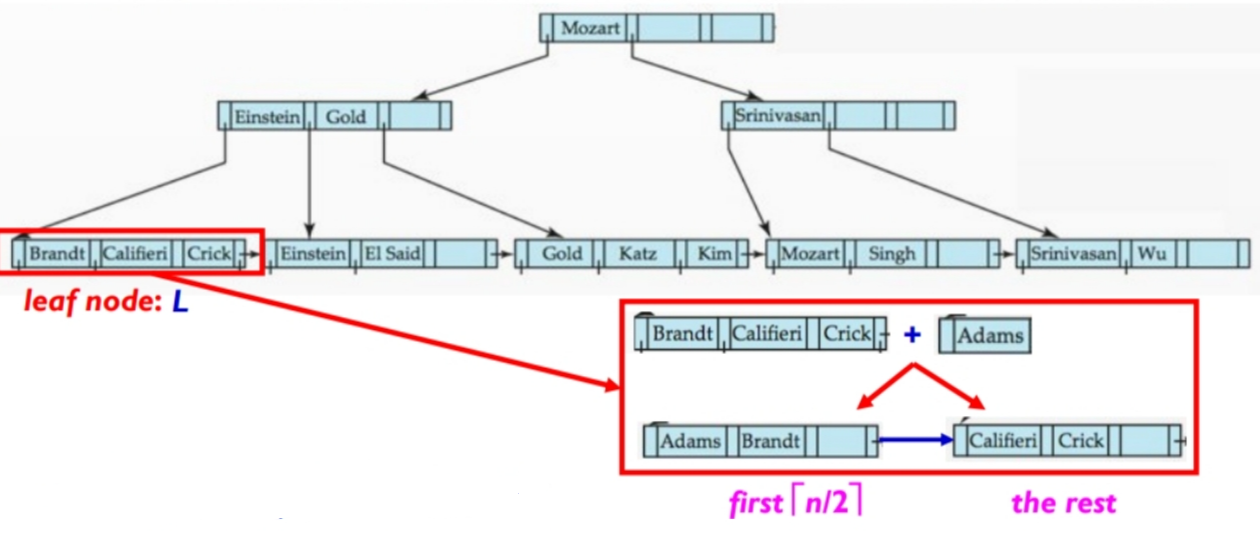
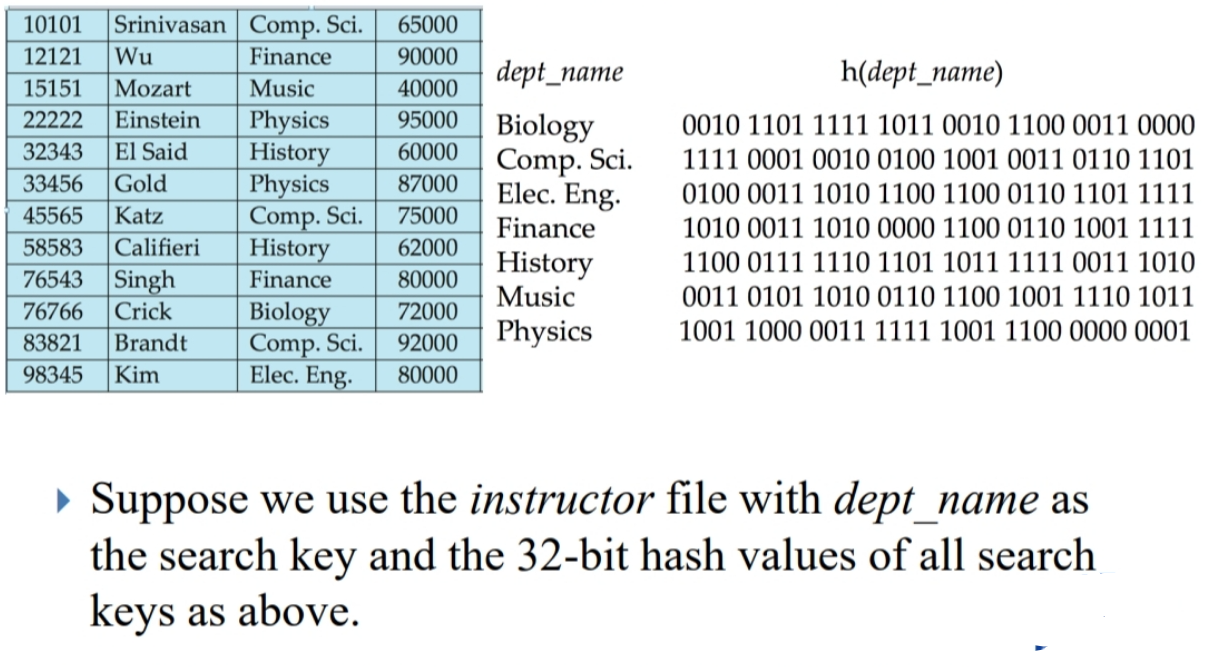
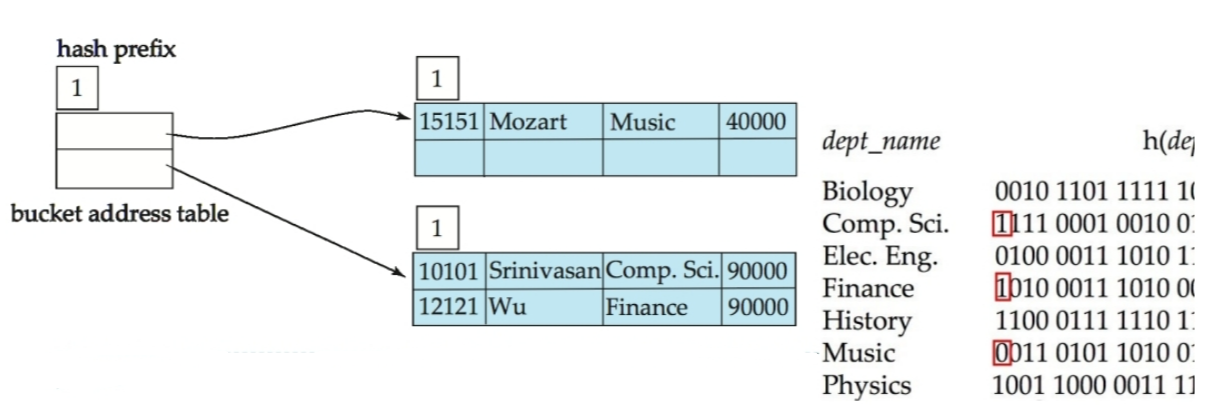
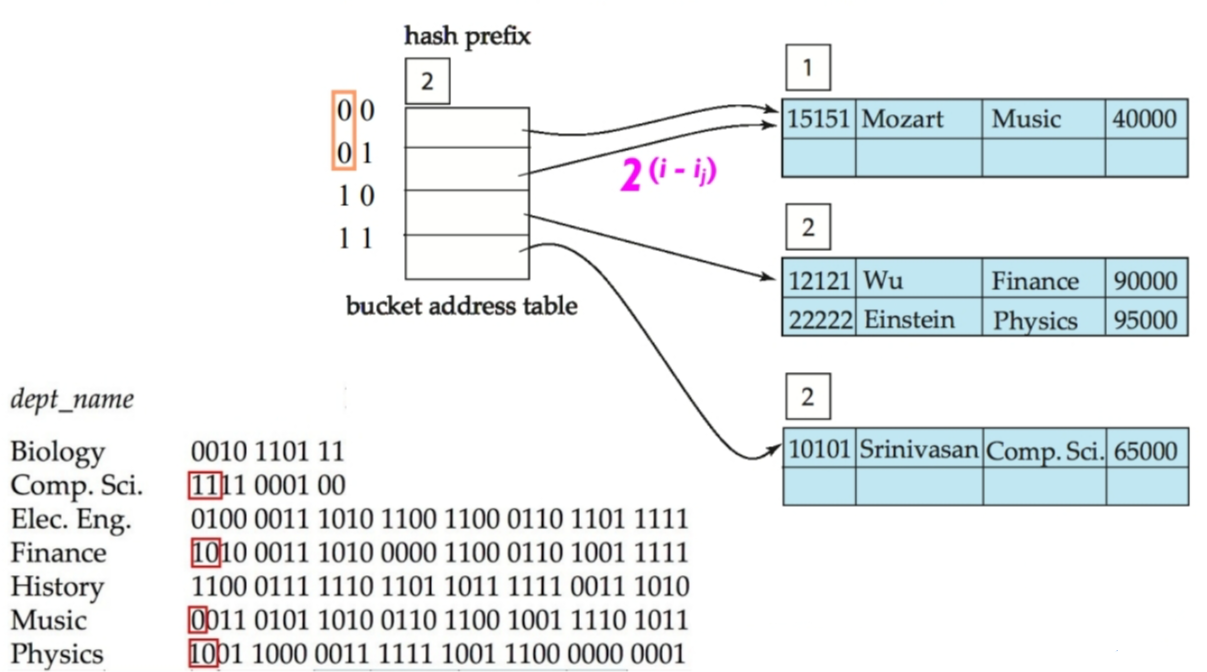
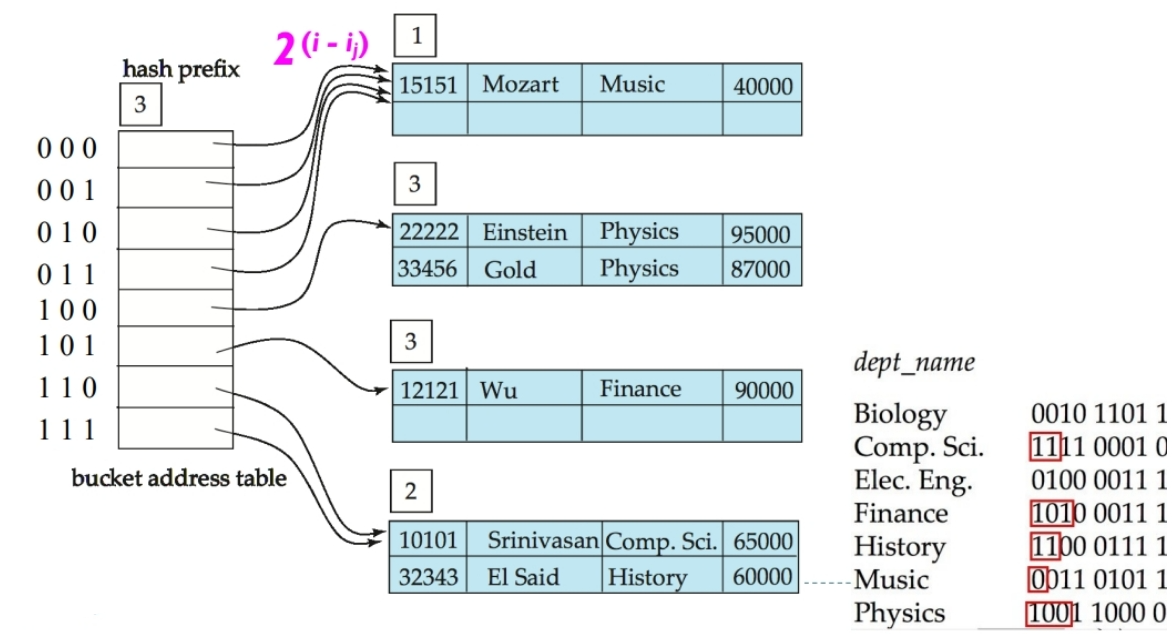
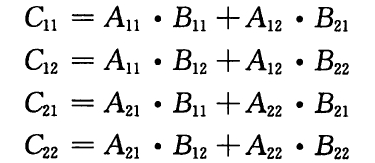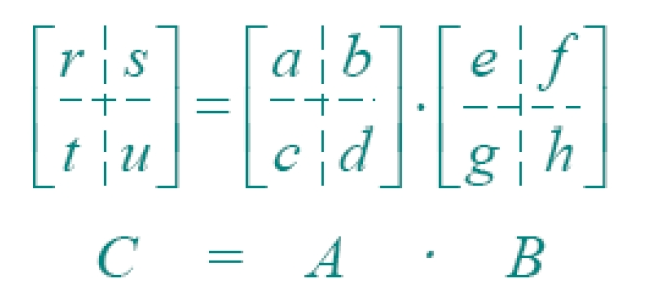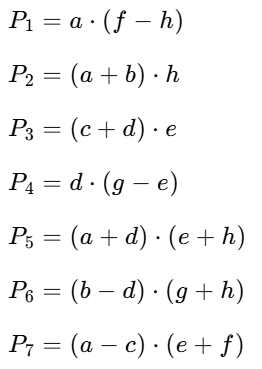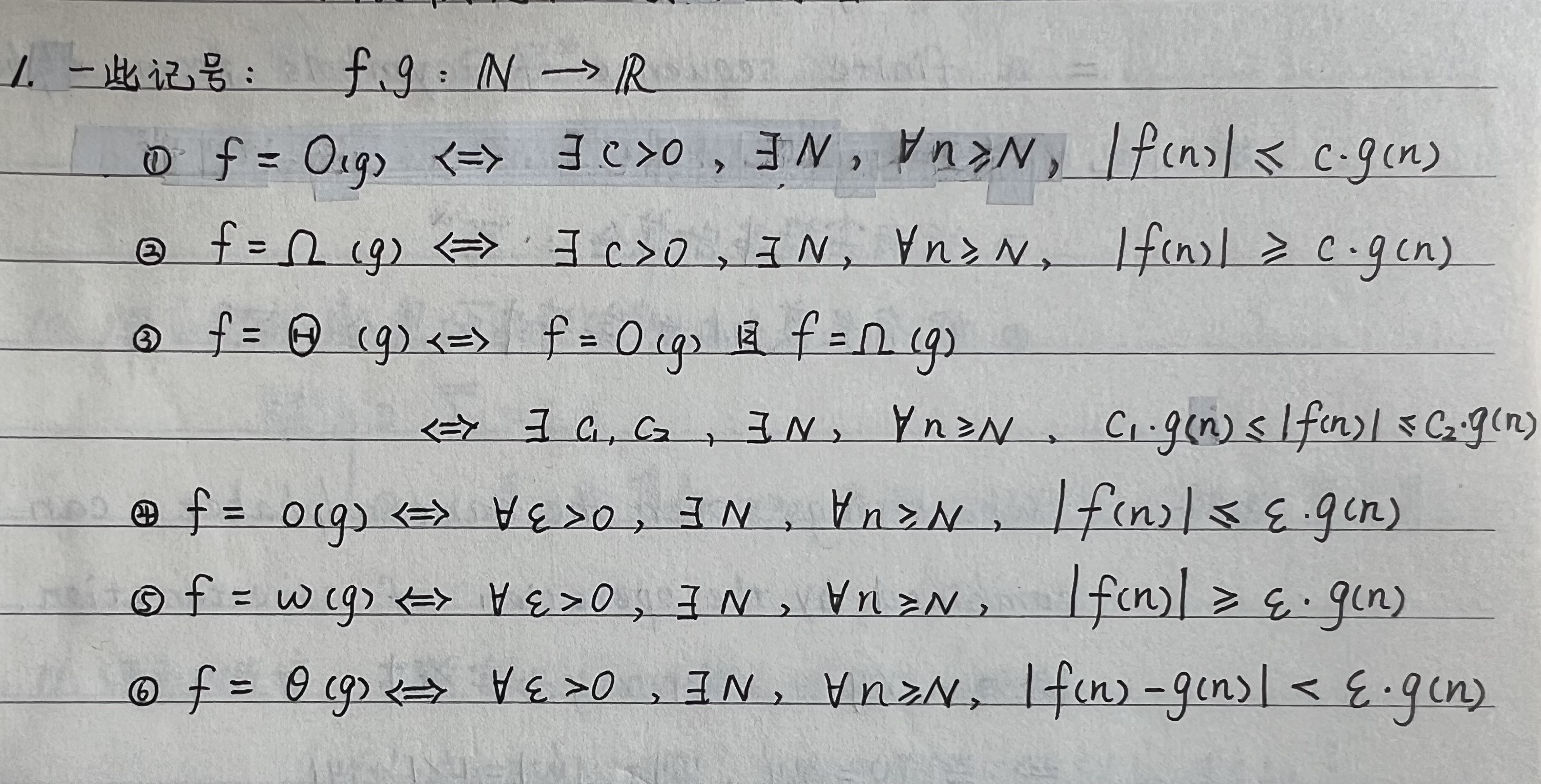延绪的水上书
0%

发表于 更新于 分类于 Disqus：

概述

动态规划（dynamic programming）与分治方法相似，都是通过组合子问题的解来求解原问题（子问题的求解是递归进行的，将其划分为更小的子子问题）。

  • 分治方法将问题划分为互不相交的子问题，递归地求解子问题，再将它们的解组合起来，求出原问题的解。
  • 与之相反，动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题。在这种情况下，分治算法会做许多不必要的工作，它会反复地求解那些公共子子问题。而动态规划算法对每个子子问题只求解一次，将其解保存在一个表格中，从而无需每次求解一个子子问题时都重新计算，避免了这种不必要的计算工作。

所以形象地说：动态规划是有记忆的分治。

动态规划方法通常用来求解最优化问题(optimization problem) 。这类问题可以有很多可行解，每个解都有一个值，我们希望寻找具有最优值（最小值或最大值）的解。可能有多个解都达到最优值。

具体来说，动态规划问题一般具有一下两个性质：

  • 最优子结构：一个问题的最优解包含其子问题的最优解。
  • 重叠子问题：问题空间必须足够“小”，即问题的递归算法会反复地求解相同的子间题，而不是一直生成新的子问题。

我们通常按如下 4 个步骤来设计一个动态规划算法：

  1. 刻画最优解的结构。
  2. 给出最优解的值的递推公式。
  3. 自底向上地计算最优解的值。
  4. 利用计算出的信息构造一个最优解。

步骤 1~3 是动态规划算法求解问题的基础。

  • 如果我们仅仅需要一个最优解的值，而非解本身，可以忽略步骤 4 。
  • 如果需要一个最优解, 有时就需要在执行步骤 3 的过程中维护一些额外信息，以便用来构造一个最优解。

所以形象地说：动态规划就是一种“数学归纳法”。

实例

斐波那契数列

如果使用一般的分治算法（递归），会有大量的重复计算。以下图为例，计算 F6 的递归过程中 F3 = F2 + F1 被重复进行了 3 次。

1
2
3
4
5
6
7
def fibonacci(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

动态规划算法为了避免重复的子问题计算，把每次计算过的子问题的解都记录下来，以后在遇到相同子问题时，直接“背答案”。

1
2
3
4
5
6
7
8
9
10
11
12
def fibonacci_dp(n):
    if n <= 0:
        return 0
    dp = [0] * (n + 1)
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

# Example usage:
n = 10
print(f"Fibonacci number at position {n} is: {fibonacci_dp(n)}")

钢条切割

问题描述：

给定一段长度为 n 英寸的钢条和一个价格表 pi (i = l, 2, …, n)。求切割钢条方案，使得销售收益 r 最大。注意：如果长度为 n 英寸的钢条的价格 Pn 足够大，最优解可能就是完全不需要切割。

长度 1 2 3 4 5 6 7 8 9 10
价格 1 5 8 9 10 17 17 20 24 30

解决办法：

首先我们将这个问题描述数学化。

如果一个最优解将钢条切割为 k 段（0 < k < n+1）, 那么最优切割方案：

将钢条切割为长度分别为 i1, i2, …, ik 的小段，得到最大收益：

考虑给出 rn 的递推公式。

切割的第一刀，可以切在任何位置。且如果是最优解，则切后的两段钢条的切割方案也一定是最优解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def cut_rod(p, n):
    # p 是价格列表，n 是钢条的长度
    r = [0] * (n + 1)

    for j in range(1, n + 1):
        max_val = float('-inf')
        for i in range(0, j + 1):
            # 计算切割后的最大收益
            max_val = max(max_val, p[i] + r[j - i])
        r[j] = max(max_val, p[j])

    return r[n]


# 价格表 & 钢条长度
prices = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
length = 10

# 计算最大收益
max_profit = cut_rod(prices, length)
print(f"最大收益为: {max_profit}")

矩阵链乘法

问题描述：

给定一个 n 个矩阵的序列（矩阵链）<A1, A2, …, An >，且矩阵 Ai 的规模为 pi-1 *pi 。求完全括号化方案（使用结合律加括号），使乘积 A1A2…An 所需标量乘法次数最少。

解决办法：

首先：用子问题的最优解来递归地定义原问题最优解。

对矩阵链乘法问题，我们可以这么定义子问题：

  • 对所有 1 <= i <= j <= n ，确定 <Ai, Ai+1, …, Aj > 的最小代价括化方案。

  • 令 m[i, j] 表示计算矩阵 Ai Ai+1 … Aj 所需标量乘法次数的最小值，那么，原问题的最优解计算 A1A2…An 所需的最低代价就是m[1, n]。

然后不难得出m[i, j]的递推公式：

m[i, j] 的值给出了子问题最优解，但它并未提供足够的信息来构造最优解。为此，我们用 s[i, j] 保存 Ai Ai+1 … Aj 最优括号化方案的分割点位置k。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def matrix_chain_order(p):
    # 矩阵的数量，p 是矩阵的维度列表
    # 创建一个二维数组 m，其中 m[i][j] 表示计算矩阵 Ai...Aj 的乘积所需的最小标量乘法次数
    # 创建一个二维数组 s，其中 s[i][j] 存储计算 m[i][j] 时最优分割点 k 的位置
    n = len(p) - 1
    m = [[0] * n for _ in range(n)]
    s = [[0] * n for _ in range(n)]
    
    # 按链的长度 l 进行处理，l 从 2 到 n
    for l in range(2, n + 1):
        for i in range(n - l + 1):
            j = i + l - 1
            m[i][j] = float('inf')
            for k in range(i, j):
                # q 表示 Ai...Ak 和 Ak+1...Aj 的乘积所需的标量乘法次数
                q = m[i][k] + m[k+1][j] + p[i] * p[k+1] * p[j+1]
                if q < m[i][j]:
                    m[i][j] = q
                    s[i][j] = k
    return m, s

def print_optimal_parens(s, i, j):
    if i == j:
        print(f'A{i+1}', end='')
    else:
        print('(', end='')
        print_optimal_parens(s, i, s[i][j])
        print_optimal_parens(s, s[i][j] + 1, j)
        print(')', end='')

# 矩阵的维度列表，例如：30*35、35*15、15*5、5*10、10*20、20*25
p = [30, 35, 15, 5, 10, 20, 25]
m, s = matrix_chain_order(p)
print("最少的标量乘法次数是:", m[0][len(p) - 2])
print("最优乘法顺序是:", end=' ')
print_optimal_parens(s, 0, len(p) - 2)

最长公共子序列

问题描述：

给定两个序列 X = <x1, x2, …, xm> 和 Y = <y1, y2, …, yn>，求 X 和 Y 最长的公共子序列。

解决办法：

首先，观察到最长公共子序列的递归结构。

我们定义 c[i,j] 表示 Xi 和 Yj 的最长公共子序列的长度。

则不难得到递推公式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def lcs(X, Y):
    # 初始化矩阵
    m = len(X)
    n = len(Y)
    c = [[0] * (n + 1) for _ in range(m + 1)]

    # 构建c矩阵
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if X[i - 1] == Y[j - 1]:
                c[i][j] = c[i - 1][j - 1] + 1
            else:
                c[i][j] = max(c[i - 1][j], c[i][j - 1])

    # 从c矩阵回溯找到LCS
    index = c[m][n]
    lcs_seq = [""] * (index)

    # 回溯找LCS
    i, j = m, n
    while i > 0 and j > 0:
        if X[i - 1] == Y[j - 1]:
            lcs_seq[index - 1] = X[i - 1]
            i -= 1
            j -= 1
            index -= 1
        elif c[i - 1][j] > c[i][j - 1]:
            i -= 1
        else:
            j -= 1

    return "".join(lcs_seq)

# 测试
X = "ABCBDAB"
Y = "BDCAB"
print(f"LCS of {X} and {Y} is {lcs(X, Y)}")

发表于 更新于 分类于 Disqus：

SSH指令

什么是SSH

SSH（Secure Shell）是一种网络协议，加密两台计算机之间的通信，并且支持各种身份验证机制。现实中，它主要用于保证远程登录和远程通信的安全，任何网络服务都可以用这个协议来加密。

SSH 密钥登录采用的是非对称加密。非对称加密需要两个密钥成对使用，分为公钥（public key）和私钥（private key）。每个用户通过自己的密钥登录。其中，私钥必须私密保存，不能泄漏；公钥则是公开的，可以对外发送。它们的关系是，公钥和私钥是一一对应的，每一个私钥都有且仅有一个对应的公钥，反之亦然。

如果数据使用公钥加密，那么只有使用对应的私钥才能解密，其他密钥都不行；反过来，如果使用私钥加密（这个过程一般称为“签名”），也只有使用对应的公钥解密。

SSH 的软件架构是服务器-客户端模式（Server-Client）。在这个架构中，SSH 软件分成两个部分：

  • 向服务器发出请求的部分，称为客户端（client），OpenSSH 的实现为 ssh。
  • 接收客户端发出的请求的部分，称为服务器（server），OpenSSH 的实现为 sshd。

另外，OpenSSH 还提供一些辅助工具软件（比如 ssh-keygen 、ssh-agent）和专门的客户端工具（比如 scp 和 sftp ），这个教程也会予以介绍。

SSH客户端

  • 安装SSH客户端：

    1
    2
    # Ubuntu 和 Debian（Linux系统一般自带ssh）
    $ sudo apt install openssh-client

  • 登录服务器：

    hostname 是主机名，它可以是域名，也可能是 IP 地址，或局域网内部的主机名。

    1
    $ ssh hostname

    不指定用户名的情况下，将使用客户端的当前用户名，作为远程服务器的登录用户名。

    1
    $ ssh user@hostname

    用户名也可以使用 ssh 的 -l 参数指定，这样的话，用户名和主机名就不用写在一起了。

    1
    $ ssh -l username host

    ssh 默认连接服务器的22端口，-p参数可以指定其他端口。

    1
    $ ssh -p 8821 foo.com

  • 配置文件：

    配置文件的格式是：

    1. 每一行是一个配置命令。每行都是配置项和对应的值，配置项的大小写不敏感，与值之间使用空格分隔。
    2. # 开头的行表示注释，# 只能放在一行的开头，不能放在一行的结尾。

    SSH 客户端的全局配置文件是 /etc/ssh/ssh_config。

    用户个人的配置文件在~/.ssh/config，优先级高于全局配置文件。

    除了配置文件，~/.ssh目录还有一些用户个人的密钥文件和其他文件。下面是其中一些常见的文件。

    文件 用途
    ~/.ssh/id_ecdsa 用户的 ECDSA 私钥
    ~/.ssh/id_ecdsa.pub 用户的 ECDSA 公钥
    ~/.ssh/id_rsa 用于 SSH2 的 RSA 私钥
    ~/.ssh/id_rsa.pub 用于SSH2 的 RSA 公钥
    ~/.ssh/identity 用于 SSH1 的 RSA 私钥。
    ~/.ssh/identity.pub 用于 SSH1 的 RSA 公钥
    ~/.ssh/known_hosts 包含 SSH 服务器的公钥指纹

    用户个人的配置文件~/.ssh/config，可以按照不同服务器，列出各自的连接参数，从而不必每一次登录都输入重复的参数。下面是一个例子。（可以写入多个服务器信息。*是通配符，表示所有服务器。）

    1
    2
    3
    4
    5
    6
    7
    8
    Host GitHub
      User git
      Hostname github.com
      IdentityFile ~/.ssh/id_rsa_keats
      
    Host *
      Port 2222
      IdentityFile ~/.ssh/id_rsa_keats

    以后，登录 remote.example.com 时，只要执行 ssh remoteserver 命令，就会自动套用 config 文件里面指定的参数。

SSH服务器

  • 安装SSH服务器：

    1
    $ sudo apt install openssh-server

  • 启动sshd：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    # 启动
    $ sudo systemctl start sshd.service

    # 停止
    $ sudo systemctl stop sshd.service

    # 重启
    $ sudo systemctl restart sshd.service

    # 让 sshd 在计算机下次启动时自动运行
    $ sudo systemctl enable sshd.service

  • 配置文件：

    sshd 的配置文件在 /etc/ssh 目录，主配置文件是 sshd_config，此外还有一些安装时生成的密钥。

    文件 用途
    /etc/ssh/sshd_config 配置文件
    /etc/ssh/ssh_host_ecdsa_key ECDSA 私钥
    /etc/ssh/ssh_host_ecdsa_key.pub ECDSA 公钥
    /etc/ssh/ssh_host_key 用于 SSH1 的 RSA 私钥
    /etc/ssh/ssh_host_key.pub 用于 SSH1 的 RSA 公钥
    /etc/ssh/ssh_host_rsa_key 用于 SSH2 的 RSA 私钥
    /etc/ssh/ssh_host_rsa_key.pub 用于 SSH2 的 RSA 公钥
    /etc/pam.d/sshd PAM 配置文件

    配置文件修改以后，并不会自动生效，必须重新启动 sshd。

SSH密钥登录

SSH 密钥登录分为以下的步骤：

  1. 客户端通过 ssh-keygen 生成自己的公钥和私钥。
  2. 手动将客户端的公钥放入远程服务器的指定位置。
  3. 客户端向服务器发起 SSH 登录的请求。
  4. 服务器收到用户 SSH 登录的请求，发送一些随机数据给用户，要求用户证明自己的身份。
  5. 客户端收到服务器发来的数据，使用私钥对数据进行签名，然后再发还给服务器。
  6. 服务器收到客户端发来的加密签名后，使用对应的公钥解密，然后跟原始数据比较。如果一致，就允许用户登录。

  • 生成密钥：

    1
    2
    3
    4
    5
    # 直接输入ssh-keygen，程序会询问一系列问题（直接回车即可），然后生成密钥。
    $ ssh-keygen

    # 使用-t参数，指定密钥的加密算法。如果省略该参数，默认使用 RSA 算法。
    $ ssh-keygen -t dsa

  • 上传公钥：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    # 生成密钥以后，公钥必须上传到服务器，才能使用公钥登录。
    # OpenSSH 规定，用户公钥保存在服务器的~/.ssh/authorized_keys文件。
    # 你要以哪个用户的身份登录到服务器，密钥就必须保存在该用户主目录的~/.ssh/authorized_keys文件。
    # 只要把公钥添加到这个文件之中，就相当于公钥上传到服务器了。每个公钥占据一行。如果该文件不存在，可以手动创建。
    # 用户可以手动编辑该文件，把公钥粘贴进去；也可以在本机计算机上，执行ssh-copy-id 命令，自动上传公钥。
    # 只要公钥上传到服务器，下次登录时，OpenSSH 就会自动采用密钥登录，不再提示输入密码。

    # OpenSSH 自带一个ssh-copy-id命令，可以自动将公钥拷贝到远程服务器的~/.ssh/authorized_keys文件。
    # 如果~/.ssh/authorized_keys文件不存在，ssh-copy-id命令会自动创建该文件。
    # 公钥文件可以不指定路径和.pub后缀名，ssh-copy-id会自动在~/.ssh目录里面寻找。

    $ ssh-copy-id -i key_file user@host

WSL安装

启用 Windows 功能：

打卡虚拟机相关功能

下载 WSL：

1
2
3
4
5
# 下载
$ wsl --install

# 查看版本
$ wsl --version

下载 Ubuntu：

在Microsoft Store随便选一个版本的Linux内核

在 Ubuntu 中配置 SSH 服务器

  • 安装 ssh 服务器

    1
    $ sudo apt-get install openssh-server

  • 运行 ssh 服务器

    1
    $ sudo service ssh start

  • 检查 ssh 服务器是否已经开启成功

    1
    $ systemctl status sshd

    如果有 active (running) 表示已经运行，否则则执行安装步骤

  • 修改配置文件

    1
    2
    3
    4
    5
    $ sudo vim /etc/ssh/sshd_config

    # 增加 `Port 22`
    # 增加 `PermitRootLogin yes`
    #如果配置文件中已经有上述两项配置，则修改

  • 查看虚拟机的 ip

    1
    $ ifconfig

Windows 中 ssh 登录

  • 打开 powershell，ssh 连接虚拟机

    1
    $ ssh <username>@<ip_address>

  • 如果登录成功，表示 linux 配置成功。否则根据输入的错误日志，重新排查。

VScode 配置

  • 安装 SSH 插件

    安装以上三个插件

  • SSH登录

    点击加号添加服务器，在上方长栏输入ssh命令，并配置客户端

    1
    2
    3
    4
    Host Ubuntu(自定义)
        HostName 10.245.68.242	（虚拟机内部系统ip地址）
        User <user_name>				（虚拟机内部系统登录账号）
        IdentityFile "C:\Users\<User_name>\.ssh\id_rsa"

  • 配置 SSH 密钥免密登录

    1. 制造密钥：

      1
      $ ssh-keygen -t rsa -C "<email>

    2. 复制密钥：

      1
      2
      # 一般位于 C:\Users\<User_name>\.ssh
      cat /rsa_id.pub

    3. 粘贴到 Ubuntu 虚拟机：

      1
      $ vim ~/.ssh/authorized_keys

  • 最终效果

    在vscode终端直接访问Ubuntu虚拟机

参考文章

SSH 密钥登录

vscode 连接本地虚拟机 Linux 系统

发表于 更新于 分类于 Disqus：

何为分治

分治算法通常用于解决递归问题，特别是在处理可以划分为相似子问题的情况下。

具体来说，分治算法分为三步（在每层递归中）：

  • 分解（Divide）：将问题划分为一些子问题，子问题的形式与原问题一样，只是规模更小。
  • 解决（Conquer）：递归地求解出子问题。如果子问题的规模足够小，则停止递归，直接求解。
  • 合并（Combine）：将子问题的解组合成原问题的解。

递归式

当我们计算分治算法的运行时间，自然地会使用递归公式来刻画。

所以如何求解递归式（求出算法运行时间的 Θ 或 O 渐近界）是很重要的。这里介绍三种方法：

  • 代入法：先猜后证，数学归纳。
  • 递归树法：画树状图。
  • 主方法：求解形如T(n) = aT(n/b) + f(n)的递归式。

代入法

代入法很朴素，就两步：

  • 猜测解的形式。
  • 用数学归纳法证明：解是对的。

例题：

T(n) = 2T(n/2) + n

题解：

1
2
3
4
5
6
7
8
9
10
11
我们猜测 T(n) = O(n·lgn)
即欲证：T(n) <= c·n·lgn, ∃c > 0

归纳假设：T(n/2) <= c(n/2)·lg(n/2), ∃c > 0
那么：
T(n) <= 2(c·n/2·lg(n/2)) + n
	 = c·n·lgn - c·n + n
	 <= c·n·lgn
	 当 c >= 1 时

综上，T(n) = O(n·lgn)。

实际上，我们可以证明：T(n) = Θ(n·lgn)。

递归树法

虽然代入法可以简洁地证明一个解确是递归式的正确解，但做出一个好的猜测可能会很困难。画递归树则适合用来生成好的猜测。

在递归树中，我们将递归式转换为一棵树：

  • 每个结点表示一个单一子问题的代价，子问题对应某次递归函数调用。
  • 我们将树中每层中的代价求和，得到每层代价。
  • 然后将所有层的代价求和，得到所有层次的递归调用的总代价。

例题：

题解：

我们一层层展开递归树：

则我们的时间总开销为：

综上：T(n) 是 n 平方量级的。

主方法

对于一些常见且特别的递归式，我们给出主定理。

主定理的证明，核心是：画递归树、分类讨论。

实例

归并排序 Vs 快速排序

归并排序和快速排序本质上都是分治算法。递推公式均是：T(n) = 2·T(n/2) + O(n)。

Divide Conquer Combine
归并排序 O(1) 2·T(n/2) O(n)
快速排序 O(n) 2·T(n/2) 0

根据主方法，我们可以知道，两者的渐近时间复杂度都是**O(n·lgn)**，都是很高效的排序方法。

但两者还是有细微的区别：

  • 快速排序实际执行的快慢是随机的，很大程度上受pivot的影响。

    最好情况是 pivot 恰好是当前子列的中位数。

    最坏情况是 pivot 是最大或者最小值，则经历一次划分，几乎没有对换，也即是：花费O(n)时间却只排好了一个元素。

  • 在数据规模不大的时候，归并排序不一定很快。这是因为：归并排序有大量递归，函数栈很深，且每次调用函数都有额外开销。

归并排序（Merge Sort）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 归并排序步骤：
# 1.Divide: Trivial.
# 2.Conquer: Recursively sort 2 subarrays.
# 3.Combine: Linear-time merge.
# 所以：T(n) = 2·T(n/2) + O(n)

def merge_sort(arr):
    if len(arr) > 1:
        # 找到中间位置，将数组分成两半
        mid = len(arr) // 2
        # 分别对两半进行归并排序
        left_half = merge_sort(arr[:mid])
        right_half = merge_sort(arr[mid:])

        # 合并两个排序好的部分，线性时间内完成（merge函数省略了）
        arr[:] = merge(left_half, right_half)
    return arr

快速排序（Quick Sort）

1
2
3
4
5
6
7
8
9
10
11
12
13
# 快速排序步骤：
# 1.从列表中选择一个元素作为“基准”（pivot）。
# 2.重新排列列表，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（等于基准值的元素可以放到任一边）。
# 3.递归地把小于基准值元素的子列表和大于基准值元素的子列表排序。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        less = [x for x in arr[1:] if x <= pivot]
        greater = [x for x in arr[1:] if x > pivot]
        return quick_sort(less) + [pivot] + quick_sort(greater)

斐波那契数列

求斐波那契数列第n项是一个非常经典的分治问题，但却有很多种不同的分治策略。

算法1：自底向上

从数列的第一项开始，一项项递推。（这也是简单的动态规划算法）

不难看出，该算法的时间复杂度是：O(n) 。

1
2
3
4
5
6
7
8
9
# python代码实现
def fibonacci_dp(n):
    if n <= 0:
        return 0
    dp = [0] * (n + 1)
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

算法2：矩阵快速幂

首先，我们注意到斐波那契数列如下的性质。

所以，“求解数列第n项”转换成：如何快速的求矩阵的幂次。

如何求幂次呢？最简单的方法是：循环n次，累乘。但这显然不是最快速的。

最快速的方法是二分算法：将 n 次幂拆分成求解 [n/2] 次幂的平方，以此类推。此时的时间开销为：**O(lgn)**。

算法3：通项公式

常言道：“暴力出奇迹”。我们可以直接计算通项公式，结果为float型，再取整即可。

1
2
3
4
5
6
7
8
# python代码实现
import math

def fibonacci_binet(n):
    phi = (1 + math.sqrt(5)) / 2
    psi = (1 - math.sqrt(5)) / 2
    return round((phi**n - psi**n) / math.sqrt(5))

矩阵乘法

计算机大量的计算是矩阵乘法。如何高效的完成两个矩阵的乘法呢？

算法1：三重循环

根据矩阵乘法的定义，我们可以在 O(n3) 内完成。

伪代码如下：

1
2
3
4
5
6
7
function MATRIX_MULTIPLY(A, B):
    # 三重循环，执行矩阵乘法
    for i = 1 to n:                  # 遍历A的每一行
        for j = 1 to n:              # 遍历B的每一列
            for k = 1 to n:
                C[i][j] = C[i][j] + A[i][k] * B[k][j]
    return C

算法2：分块矩阵

简单起见，我们将 n 阶矩阵划分为4个 n/2 阶矩阵，以此递归。

则我们每次递归需要的时间开销：

  • 划分分块矩阵
  • 递归计算A、B的8个子矩阵乘积
  • 求和得到C11、C12、C21、C22。
Divide Conquer Combine
T(n) O(1) 8·T(n/2) 4·( n/2 )2 = O(n2)

但非常遗憾，根据主方法，如此二分算法的时间开销仍是：**O(n3)**。

如何更快速呢？

核心在于：每次递归时，计算尽可能少的矩阵乘法，再通过加法组合出我们想要的子矩阵。（因为：矩阵乘法是 O(n3)，而矩阵加法是 O(n2)。）

对此，我们如下改进：

我们只计算如下7个矩阵乘法。

再通过加法，算出C矩阵。

  • r = P5 + P4 − P2 + P6
  • s = P1 + P2
  • t = P3  + P4
  • u = P5 + P1 − P3 − P7

此时算法的时间开销是：**O(nlog27)**。

发表于 更新于 分类于 Disqus：

函数增长

在比较算法性能时，虽然有时我们能够确定一个算法的精确运行时间，但是通常并不值得花力气来计算它（精度多余了）。对于足够大的输入，算法的运行时间中的常数倍数和低阶项相对于输入规模的影响变得不那么显著。

因此，我们研究渐近效率。我们关心：当输入规模无限增加时，在极限中，算法的运行时间如何随着输入规模的变大而增加。

渐近记号

以下是常用的渐近记号。

对于两个函数f、g的渐近比较，我们可以将其类比成实数a、b的比较。

发表于 更新于 分类于 Disqus：

预备知识

一段代码，从 .c 源文件到可执行文件经历了4个步骤：

  • 预处理（Preprocessing）：主要处理源代码中以#开始的预编译指令，比如#include、#define 等等。预处理完得到的是.i文件。
  • 编译（Compilation）：编译完成后，得到的是：汇编文件（.s）
  • 汇编（Assembly）：将汇编代码转换成机器可以执行的指令，每一条汇编指令都会对应一条机器指令。汇编完成后，得到的是：可重定向目标文件（.o）。
  • 链接（Linking）：通常一份文件会调用其他文件中编写的函数，但当前文件怎么知道去哪里寻找它想调用的函数呢？这就需要链接。链接完成后，得到的是：可执行目标文件。

其中：可重定向目标文件、可执行目标文件都必须符合ELF格式（Executable and Linkable Format），因此也可称为：ELF文件。

ELF文件包含一下三个部分：

  • ELF header
  • Sections
  • Section header table

下图是一个 Hello World 可执行程序的 ELF 格式实例。

ELF

我们可以通过命令行工具readelf查看 elf 文件。

1
$ readelf -h demo   #查看elf header

ELF header

1
$ readelf -S demo   #查看各个section信息

Sections

这里容易混淆的是：ELF Header、Program Header、Section Header：

  • ELF Header 是 ELF 文件的文件头，它是文件的起始部分，为加载器和链接器提供必要的信息来处理文件。
  • Program Header 是一个数据结构，它定义了程序如何加载到内存中。每个 Program Header 都包含了一个段（Segment）的加载信息，比如它的类型、在文件中的偏移量、在内存中的地址、大小等。
  • Program Header Table 是一个由多个 Program Header 组成的数组，它按照程序头的顺序排列。Program Header Table 通常位于 ELF Header 之后，通常在文件的开始部分，这样加载器可以快速地找到并读取它。
  • Section Header 定义了文件中的节（Section）的属性和信息。每个节头条目（Section Header Entry）都包含了关于一个特定节的元数据。

注意：

Sections 中的第一个 Section（索引为0的section）就是 Program Header Table。

以之前图中 ELF 文件为例。

**ELF Header **占据最开始的64个字节。

紧接着是Program Header Table，总共占据 56 * 13 = 728个字节。

所以真正的第一个section（.interp）开始地址应该是：64 + 728 = 792 = 0x318。

另外一个容易混淆的是：节（Section）、段（Segment）。

  • Section 称为节，是指在汇编源码中经由关键字section或segment修饰、逻辑划分的指令或数据区域，汇编器会将这两个关键字修饰的区域在目标文件中编译成节，也就是说”节”最初诞生于目标文件中。

  • Segment 称为段，是，链接器把目标文件链接成可执行文件，因此段最终诞生于可执行文件中。我们平时所说的可执行程序内存空间中的代码段和数据段就是指的Segment。

Section Vs Segment

  • 左边是ELF的链接视图，可以理解为是目标文件的内容布局。
  • 右边是ELF的执行视图，可以理解为可执行文件的内容布局。

注意：目标代码文件的内容是由 Section 组成的，而可执行文件的内容是由 Segment 组成的。

  • 我们查看汇编程序时，.text，.bss，.data 都指的是 Section。目标代码文件中的 Section 和 Section Header Table 中的条目是一一对应的。Section 的信息用于链接器对代码重定位。

  • 而文件载入内存执行时，是以 Segment 组织的，每个 Segment 对应 ELF 文件中 Program Header Table 中的一个条目，用来建立可执行文件的进程映像。链接器将目标文件中属性相同的多个 Section 合并，从而形成新的可执行文件；合并后的 Section 的集合，称为 Segment。例如：所有.text Section 会被合并成一个新的.text Segment。

注意：在目标文件中，Program Header 不是必须的，我们用 gcc 生成的目标文件也不包含 Program Header。

在所有Sections中，有一个section比较特殊：.shstrtab。

Section Header String Table

在之前查看 ELF Header 的时候，ELF Header 就提供了 .shstrtab Section 的索引是多少。

  • 节头字符串表（Section Header String Table，简称SHSTRTAB）是 ELF 文件中的一个特殊 section。它包含所有 section 名称的字符串。

  • 每个 Section Header 中的sh_name字段是一个索引，指向节头字符串表中的一个位置，该位置存储了该 section 的名称。

  • 节头字符串表本质上是一个以空字符（\0）分隔的字符串集合。每个section的名称在这个表中都有一个唯一的偏移量，该偏移量存储在对应section头部的sh_name字段中。

    1
    2
    3
    4
    0x00: "\0"
    0x01: ".text\0"
    0x07: ".data\0"
    0x0D: ".bss\0"

技术路线

我们希望采用跳板技术实现静态插桩。

  • 跳板技术：简单来说，就是通过设置一个中间点（跳板），让程序先跳到这个中间点，然后由这个中间点再跳到最终的目标函数去执行。这个过程就像是设置了一个中转站，让程序先到中转站，再由中转站引导到目的地。
  • 我们给目标程序新增加一个section作为跳板（trampoline）。

具体分为两个函数：

  1. 创造trampoline空间的函数：Crt_Trpline
  2. 进行二进制插桩的函数： Sinsert
  3. 复原函数：recover

代码实现

bfd.pdf

在BFD（Binary File Descriptor）库中，bfd_make_section 及其相关函数用于创建新的节（section）并将其附加到BFD（Binary File Descriptor）结构中。这些函数提供了不同的选项和功能，以适应不同的使用场景。以下是一些常见的 make section 函数及其区别和功能：

  1. bfd_make_section

    • 功能：创建一个新的空节，并将其附加到BFD的节链表中。
    • 参数：只需要提供BFD和节的名称。
    • 特点：如果同名节已存在，则不会创建新的节，而是返回现有的节。

  2. bfd_make_section_anyway

    • 功能：创建一个新的空节，即使同名节已存在，也会创建新的节，并附加到BFD的节链表中。
    • 参数：提供BFD和节的名称。
    • 特点：不检查是否已存在同名节，总是创建新的节。

  3. bfd_make_section_with_flags

    • 功能：创建一个新的节，并为其设置特定的标志（flags）。
    • 参数：提供BFD、节的名称和要设置的标志。
    • 特点：允许在创建节时指定节的属性，如是否可加载、是否可执行等。

  4. bfd_make_section_anyway_with_flags

    • 功能：创建一个新的节，并为其设置特定的标志，即使同名节已存在。
    • 参数：提供BFD、节的名称和要设置的标志。
    • 特点：结合了 bfd_make_section_with_flags 和 bfd_make_section_anyway 的功能。

  5. bfd_make_section_old_way

    • 功能：使用旧方法创建一个新的节。
    • 参数：只需要提供BFD和节的名称。
    • 特点：如果同名节已存在，则不会创建新的节，而是返回现有的节。这是较老的API，可能在新版本的BFD中不再推荐使用。

  6. bfd_set_section_flags

    • 功能：设置现有节的标志。
    • 参数：提供节和要设置的标志。
    • 特点：不创建新节，只修改现有节的属性。

  7. bfd_set_section_size

    • 功能：设置现有节的大小。
    • 参数：提供节和新的大小。
    • 特点：不创建新节，只修改现有节的大小。

  8. bfd_set_section_contents

    • 功能：设置现有节的内容。
    • 参数：提供BFD、节、数据缓冲区、偏移量和数据大小。
    • 特点：不创建新节，只修改现有节的内容。

这些函数提供了灵活的方式来创建和管理BFD中的节。选择哪个函数取决于你的具体需求，比如是否需要检查同名节的存在、是否需要设置特定的节属性等。在实际应用中，应根据目标文件格式和操作需求选择合适的函数。

1

如何新增section

我们主要通过c语言标准库中提供的工具来编辑 elf header。

1
2
3
#include <elf.h>
#include <libelf.h>
#include <gelf.h>

发表于 更新于 分类于 Disqus：

引言

就像查字典有拼音索引、部首索引、笔画索引一样，为了方便查询，数据库中也有索引。主要有以下两种索引：

  • 顺序索引（Ordered indices）
  • 哈希索引（Hash indices）

首先，我们介绍一些预备知识。

查询记录时，我们会根据一个属性或者多个属性进行搜索。这个属性集，我们称为：搜索码（search key）。

索引包含若干索引项。索引项（index entry）由一个搜索码值和指向记录的一个或多个指针构成。

考虑到：数据库中更新记录，可以等价为先删除旧记录，在插入新记录。所以，我们只需要考虑插入索引和删除索引即可。

顺序索引

在顺序索引中，索引项是按照 search key 进行排序存储的。

但是数据的存储顺序不一定与索引项的排序顺序相同。所以，根据是否与数据的排序顺序相符合，我们将索引分为两类：

  • 主索引（ Clustering Index）：索引顺序与数据顺序相同。

  • 辅助索引（Non-clustering Index）：索引顺序与数据顺序不同。

    secondary index

除了这种分类方式，还可以根据索引项的密度进行分类：

  • 稠密索引（Dense Index）：每一个搜索码都对应地有一个索引项。

    dense index (but not clustering)

  • 稀疏索引（Sparse Index）：索引项只涵盖了部分搜索码的可能取值。

    sparse index

请注意：辅助索引必须是稠密索引，即每个搜索码都有一个索引项。这是因为：辅助索引的顺序与数据顺序不同，如果一个搜索码没有对应的索引项，那么这个记录可能出现在数据库中的任何地方，那么索引也就失去作用了。

显然，如果索引是聚集且稀疏的，查询一个记录则可以这么做：先在索引中寻找不大于当前搜索码值的最大索引，在从这个索引项指向的记录开始，依次往后搜索。

所以，稀疏索引的好处时可以使用更少的空间来存储索引，但定位一个记录的时间会更慢一点。所以一个不错的权衡是：生成一个稀疏索引，为每一个块建一个索引项（generate a sparse index with an index entry for every block in file）。

B+树索引

优缺点

B+树索引的好处和缺点如下：

优点 缺点
每次插入删除会自动重组索引结构 每次插入删除都有额外的时间开销
不需要重组整个文件来维持性能 维持B+树的空间开销

整体结构

中间节点（internal nodes）：既不是根节点，也不是叶节点

B+树是一个有根节点的树，且满足以下性质：

  • 所有从根节点到叶节点的路径都一样长。（平衡树）
  • 每个中间节点有 ⌈n/2⌉ 到 n 个子节点。（n预先给定的）
  • 叶节点有 ⌈(n-1)/2⌉ 到 n-1个值。
  • 如果根节点不是叶节点，则根节点至少有两个子节点。
  • 如果根节点是叶节点，则根节点有 0 到 (n-1) 个值。

B+ tree 1

B+ tree 2

节点结构

对于非叶子节点：

B+ tree node structure

其中：

  • 指针个数 n 称为：扇出（fanout）。

  • **K1 < K2 < …… < Kn-1**（假设搜索码不会重复）

    K-condition

如果是叶子节点，则还有如下性质：

  • 最后一个指针 Pn 指向下一个叶子节点。
  • Pi 指向的记录的搜索码取值为 Ki 。
  • 如果叶节点 Li < Lj ，那么叶节点 Li 中所有记录的搜索码都小于等于 Lj 中的。

如果搜索码可能重复，那么 Ki 序列不再是严格单增的。而是：K1 <= K2 <= …… <= Kn-1

查询

在 B+ 树种查找搜索码为 V 的记录，方法如下（伪代码表示）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
set C = root node

while(C is not a leaf node) {
    Let i = smallest number s.t. V <= C.Ki
    if no such i exists, then set C = C.Pm
    	where Pm = last non-null pointer in the node
    else if(V = C.Ki) then set C = C.Pi+1
    else set C = C.Pi
}

Let i be the least value s.t. Ki = V

if there is such a value i, return (C, i)
else return null

query example

更新

由于 B+ 树对每个节点的子节点数有限制，所以每次插入删除都可能需要：

  • Split a node if the node becomes too large.
  • Coalesce (合并) two or more nodes if a node becomes too small.

分裂和合并的规则描述起来比较复杂，我们直接看例子。

  1. 插入”Adam”：

    • 先根据之前的查询的流程来定位。

    • 插入“Adam”，检查是否需要分裂。若需要，则分裂。

    • 子节点分裂可能导致父节点也需要分裂，所以需要一层层向上检查。

      locate the node

      split the node

      split result

  2. 在1的基础上，再插入“Lamport”：

    • 与之前类似，不过这次插入导致上层节点也需要分裂。

    insert result

  3. 删除“Srinivasan”：

    • 删除目标节点。
    • 如果删除后子节点数不符合要求，那么与兄弟节点进行合并。
    • 合并后，父节点可能也需要合并，所以需要向上一层层检查。

    delete example1

  4. 再删除“Singh”和“Wu”：

    delete example2

  5. 再删除“Gold”：

    delete example3

B 树索引

B 树类似于 B+ 树。B 树要求：每个搜索码的取值只能出现一次，从而消除重复储存搜索码的值。

B tree

B 树优点在于：

  • 使用了更少的节点
  • 可能更快地找到搜索码的值（因为不一定要遍历到叶节点）

B 树缺点在于：

  • 只有很小一部分的搜索码的值是可以更快找到的。
  • 插入和删除操作都会更复杂
  • 实现也更加麻烦

总的来说，B树不如B+树，缺点远胜优点。

哈希索引

之前的索引方式都需要建立一种索引结构，但哈希索引则可以避免：

  • 通过计算哈希函数（hash function），可以由 search key 计算得到包含目标记录的块地址。
  • A bucket is a unit of storage containing one or more records typically a disk block.

静态哈希

在静态哈希种，桶的数量是固定的。

常见的哈希函数都是：计算搜索码的二进制表示，再模上桶的数量。

例如下图中：根据dept_name，在instructor表上建立哈希索引。

桶个数=8。

哈希函数是：将各字母在字母表中的序号相加，再 mod 8。

static hash

溢出桶

但如果插入记录时，发现桶里已经装满了记录，这就是：桶溢出（Bucket Overflow）。一般有如下两种原因：

  • 桶确实不足。即使所有桶全部装满，也装不完全部记录。
  • 很多记录都装进了同一个桶，而其他很多桶还有很多空间。（Skew in distribution of records）

解决办法也很朴素：加桶（谁溢出，谁加桶）。

overflow bucket

动态哈希

静态哈希虽然易于实现，但缺点也明显：桶的数量是固定。

  • 如果设置的太小，那么需要不停的添加溢出桶，且一个 hash地址 中的记录也会非常多，导致查询效率降低。
  • 如果设置的太大，在数据规模还没起来时，大量空间被浪费了。

所以我们希望：桶的数量能动态变化。这便是：动态哈希。

这里，我们主要介绍：可扩充散列（Extendable Hashing）。

可扩充散列的核心思想是：当存储的记录不多时，我们只使用 hash 值的前几位。当存在有桶溢出的情况时，我们再使用更多的 hash 值位数。

严格来说：

  • 假定 hash 函数产生的 hash 值是 b 位。
  • 设每个桶所对应的 hash 值是 i 位，（0 <= i <= b）。
  • 当一条记录经过 hash 函数计算得的 hash 值的前 i 位与桶的 hash 值相同时，这条记录存储在这个桶里。
  • 当这个桶溢出时，这个桶会分成两个桶。它们的 hash 值都是 i+1 位，且前 i 位继承原来桶的 hash 值，最后一位则分别时0、1。原来桶中的记录依据 hash 值分别装进新的两个桶中。

具体来说，我们举例说明：

example

  • 插入“Mozart”：

Insert Mozart

  • 插入“Einstein”：

    这时2号桶的 i2 需要加1，且 bucket address table 的前缀长度 = max { ik | k = 1, 2, … , b} 也会随着加1。

Insert Einstein

  • 插入“Gold”：

Insert Gold

一些比较

如果是范围搜索，顺序索引更好。

range query

如果是搜索某个具体的值，哈希索引更好。

query based on a key

位图索引

位图索引（Bitmap Index）是一种特殊但非常高效的索引。但它一般只建立一个属性上，且该属性的可能取值很少（比如：性别、国家、省）。

具体来说：

  • 这个属性的每一个取值都有相应的 bitmap。
  • 一个取值 V 的 bitmap 的第 i 位为1，表示第i条记录的该属性是 V。若是0，则不是 V。

bitmap

发表于 更新于 分类于 Disqus：

引言

当数据库中多个事务并发执行时，事务的隔离性不一定能保持。为了保持事务的隔离性，数据库必须控制不同事务之间的互动。

这里我们将介绍两种常见的并发控制（concurrency control）的机制：

  • two-phase locking（二相锁）
  • timestamp（时间戳）

二相锁

就像“编辑在线文档”，为了避免自己写的内容被其他人篡改，最简单的方式就是：在自己编辑的时候给文档上锁，只有自己能修改其中的内容。等到修改完成后，再打开锁，允许其他人进行修改。

数据库中也是类似的。

什么是锁

数据项可以被加上以下两种模式的锁：

  • 共享锁 shared mode (S)：数据项只能被读。
  • 排他锁 exclusive mode (X)：数据项可以被读或者写。

显然，多个事务可以同时持有同一个数据的共享锁。但若有一个事务持有这个数据的排他锁，那么其他事务不能再持有该数据的共享锁。所以，不同锁之间也是存在兼容性（Lock-compatibility）的。

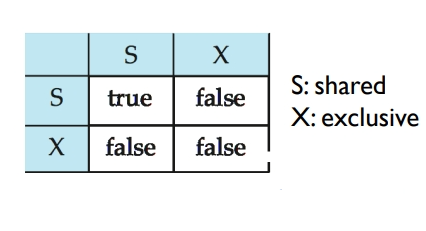
Lock-compatibility

当一个事务想访问一个数据时，它会向并发控制管理器（concurrency-control manager）发出请求。如果当前不存在与其不兼容的锁，则向该事务授权新锁；否则需要等待不兼容的锁全部被释放，才能再授权新锁。

基于锁的协议

但需要注意：上锁并不能保证调度是可序列化的。

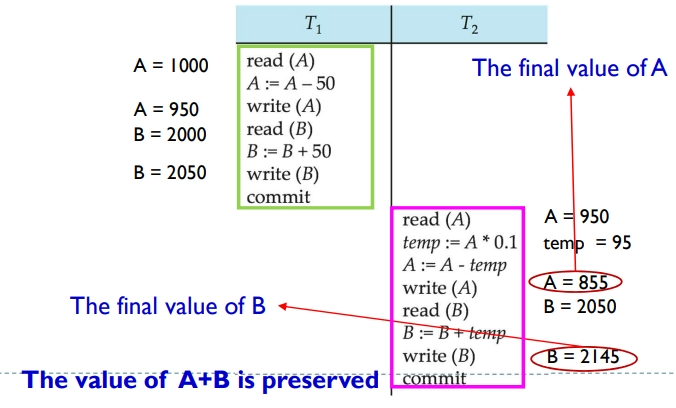
例如：A账户有100元，B账户有200元；T1是从B向A转账50元，T2是打印A、B账户金额总和。具体调度如下图。

example1

可以发现，这样的调度就不满足事务的一致性。原因在于：

  • T1 过早的释放了数据B的锁。这导致 T2 误以为自己已经获得了所有需要的数据，就开始执行。但 T2 读取的A并不是 T1 更新后的值。

因此我们还需要：基于锁的协议（Lock-Based Protocols）来对申请和释放锁进行规定。（所谓协议，就是一些需遵守的规则罢了）

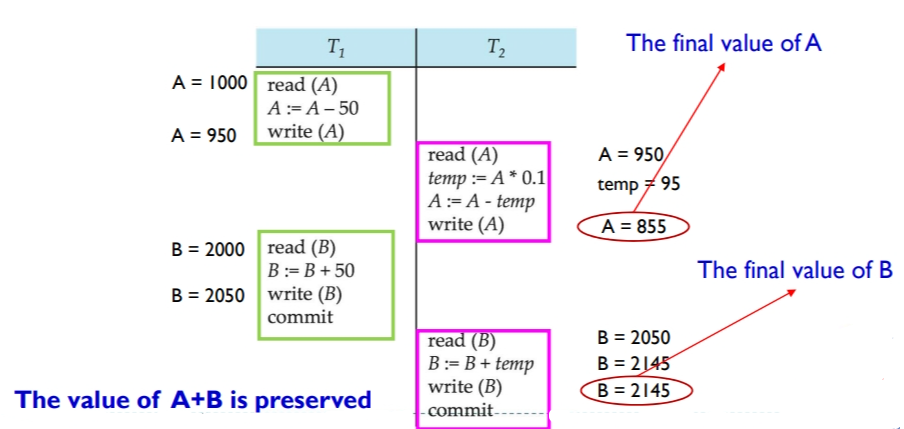
所以，针对上面例子，我们可以规定：释放锁被推迟到事务结束时。这样就能确保调度时可序列化的。

Unlocking is delayed to the end of the transaction.

死锁

当我们使用锁时，可能出现以下这种情况：

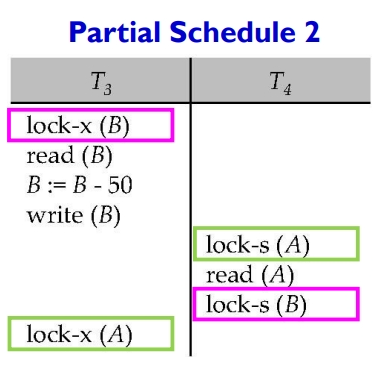
deadlock

T3 和 T4 都需要数据 A、B。但 T3 持有B并给B上锁；T4 持有A并给A上锁。此时，T3 和 T4 都有彼此想要的数据项，但又都不愿意释放出自己手中的数据。于是调度就僵持在这里，无法进行。这种情况，我们称之为：死锁（deadlock）。

就像《剪刀手爱德华》里说的：“如果我没有刀，我无法保护你；如果我拿着刀，我无法拥抱你。”如果不采用锁，无法保证事务的一致性；但如果采用锁，又会产生死锁的情况。

“两害相权取其轻”。相较于数据的不一致，死锁是可以接受的。 处理死锁的思路一般有两种：

  • 预防：采用 deadlock prevention protocol，保证系统永远不会进入死锁状态。
  • 修复：允许系统进入死锁状态，进入后进行恢复就好。

当系统有很高频率进入死锁状态时，“预防”是更好的选择。否则“进入后再恢复”是更高效的方案。

死锁预防（deadlock prevention）有以下两种常见方式：

  • 一个事务在执行的开始就把所有需要的数据上锁。要么一次性锁住所有需要的数据，要么一个也不锁。
  • 系统给所有资源分配一个全局的顺序号，事务必须按顺序请求资源。也就是说：如果一个事务已经持有了一个资源，它只能请求顺序号更大的资源，不能请求顺序号更小的资源。但如果一个事务需要请求顺序号更小的资源，它必须：1. 释放当前持有的所有锁；2. 按照顺序从小到大重新申请所有所需的资源。

第一种策略易于实现，但缺点明显：在事务的开始时，系统难以预测它究竟需要哪些数据；其次这样的数据利用效率非常低。

第二种策略可能不那么易于理解，我们举一个例子：

假设有三个资源 A、B 和 C，它们的顺序号分别是 1、2 和 3。

  • 事务 T1 需要锁定资源 B 和 A。
  • 事务 T2 需要锁定资源 A 和 B。

此时事务 T1 已经锁定资源 B，事务 T2 已经锁定资源 A。但由于 资源A顺序 < 资源B顺序 ，事务 T1 不能锁定 A，所以它会释放资源 B，重新请求上锁，这样事务 T2 就能顺利获得资源 B，从而避免死锁。

这种策略的优势在于：易于实现，不需要对底层的并发控制系统进行修改。

死锁恢复一般采用抢占和回滚（preemption and transaction rollbacks）：其实就是，抢走一个事务手中的锁，并将这些锁给其他事务，并将被抢的事务回滚。但是谁抢走谁呢？这就需要一个判断标准：事务的时间戳（Transaction timestamps）。

形象地比喻就是“银行办理业务”：每个人都会到大厅机器上取一个号码，这个就是你的时间戳。大家根据时间戳先后决定谁先办理业务。

在数据库中也是相似的，一般有两种策略：

  • Wait-Die Scheme（new-die & old-wait）：如果一个较老的事务请求一个被较新的事务持有的资源，那么较老的事务会等待。如果一个较新的事务请求一个被较老的事务持有的资源，那么较新的事务会被回滚。
  • Wound-Wait Scheme（new-wait & old-die）：如果果一个较老的事务请求一个被较新的事务持有的资源，那么较新的事务会被立即回滚。如果一个较新的事务请求一个被较老的事务持有的资源，那么较新的事务会等待。

举例说明一下：

  • 事务 T14、T15 和 T16 的时间戳分别为 5、10 和 15。
  • 在 Wait-Die 方案下：如果 T14 请求一个由 T15 持有的数据项，那么 T14 将会等待。如果 T16 请求一个由 T15 持有的数据项，那么 T16 将会被回滚。
  • 在 Wound-Wait 方案下：如果 T14 请求一个由 T15 持有的数据项，那么数据项将从 T15 中被抢占，T15 将会被回滚。如果 T16 请求一个由 T15 持有的数据项，那么 T16 将会等待。

但这两种策略都会带来不必要的回滚。

还有一种解决死锁的方式：锁超时（lock-timeout）：申请锁的事务最多等待一定时间，如果没有得到锁，则该事务自动回滚，并重启。

这种方式介于预防和恢复之间。但超时的时间限制（timeout interval）是不好把握的。太长，死锁卡住的时间就久；太短，一个事务太没耐心，从而可能不停回滚。

饿死

当我们使用锁时，会出现以下这种情况：

  • 一个事务可能在等待某个数据的排他锁，同时，许多其他事务请求并获得了该项目上的S锁（共享锁）。

形象的比喻就是“银行业务办理窗口”：

  • 事务比作人，数据比作窗口，若干事务正在排队访问数据。你前面有一个人正在读数据，但你是想写数据，你只能等待。这这时后面的人说：“嘿，我就读数据，让我凑过去看一眼”，于是他插队到你前面（获得了共享锁）。后面所有想读数据的人，都能这样插队到你前面。即使最开始的读数据的人已经完成离开了，但还有新的人正在读数据。如此，你就一直无法获取到写数据的排他锁。

这种情况，我们称之为：饿死（Starvation）。

避免这样的“插队”问题，也是很简单的——遵守“先来后到”的规则就好。具体如下。

当事务T请求数据Q的M型锁时，并发控制管理器授权加锁的条件是：

  • 此时，数据Q上没有与M不兼容的锁
  • 此时，不存在 “正在等待加锁的” 且 “排队在事务T之前的” 的事务。

二相锁协议

在 two-phase locking protocol 中：释放锁不必须在事务结束时进行。

二相锁协议是能保证调度可序列化的。它要求每个事务分两个阶段提出加锁、解锁的申请：

  • growing phase：事务只能获得锁。
  • shrinking phase：事务只能释放锁。

例如下图中：T1 和 T2 就不是二相锁，T3 和 T4 就是二相锁。（且将unlock(B)提前到lock-X(A)后面执行，也仍是遵守协议的）

example2

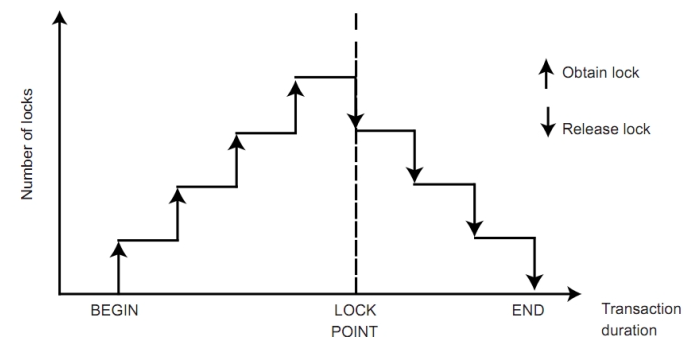
对于任何事务，它获得它的最后一个锁的时候，也就是增长阶段结束的时候，我们称之为：事务的封锁点（lock point）。

二相锁是可序列化的，且：各个事务实际上就是按照 lock point 的先后进行顺序执行完成的。

two phase lock

但二相锁并不是完美的：

  • 二相锁不能避免死锁的问题。
  • 二项锁不是无级联的。它仍然可能出现级联回滚（cascading roll back）的情况。

为了避免级联回滚，我们可以提出更严格的二相锁协议：

  • Strict two-phase locking protocol：一个事务必须持有 所有的排他锁 直到它提交或中止。
  • Rigorous two-phase locking protocol：一个事务必须持有 所有锁 直到它提交或中止。

其中后者的序列化的顺序是按照事务的提交时间（而不再是lock point）。

锁的转换

共享锁和排他锁时可以相互转换的，通过升级（upgrading）和降级（downgrading）。

例如：当事务T已经拥有S锁，且又需要X锁时：它可以将S锁升级成X锁。

conversion

但锁的升级和降级不是能乱来的：

  • 升级只能发生在 growing phase
  • 降级只能发生在 shrinking phase

且进行锁转换时也需要注意：是否与当前已有的锁兼容。若不兼容，则需要等待。

所以，当一个事务需要锁时，并不是直接申请，而是先检查是否已有锁。若有，则请求升级或者降级；若无，再申请加锁。

大部分数据库都采用 Strict two-phase locking protocol 和 lock conversion 的机制。

锁管理器

锁管理器（lock manager）就是一个进程，并维护一个记录已有锁和等待锁的数据结构——锁表（lock table）。各个事务向其发送加锁、解锁的请求。

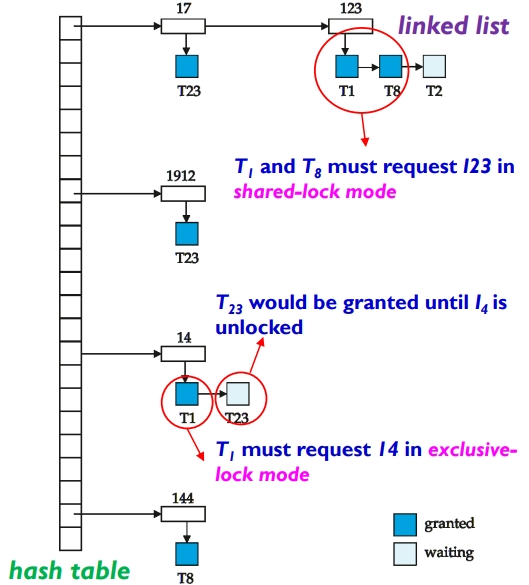
锁表结构如下图所示：

  • 用哈希链表存储各个数据项17、123、1912、14、144
  • 某一个数据项上的锁，存储在指向当前数据项的链表中。第一个是被授权的锁，后续的是正在等待的锁。
  • 例如：T2 申请 “数据123” 上的排他锁，此时 T1 和 T8 已持有其共享锁。那么 T2 的申请会被添加到 “数据123” 的链表的末尾。
  • 如果一个事务终止（aborted），锁管理器会释放该事务持有的所有锁。

lock table

多粒度

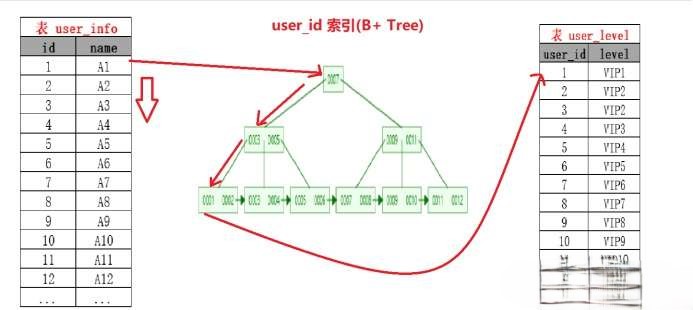
截至目前，我们讨论的并发控制都是以一个个数据为单位，但实际情况中，一个事务可能请求访问整个数据库的内容，这时一个个数据的上锁会非常耽误时间，我们希望能直接一次请求就能锁住整个数据库。所以，我们需要根据各种数据项大小，定义数据粒度的层次。

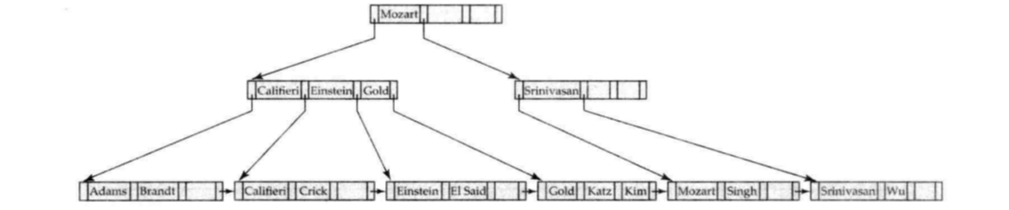
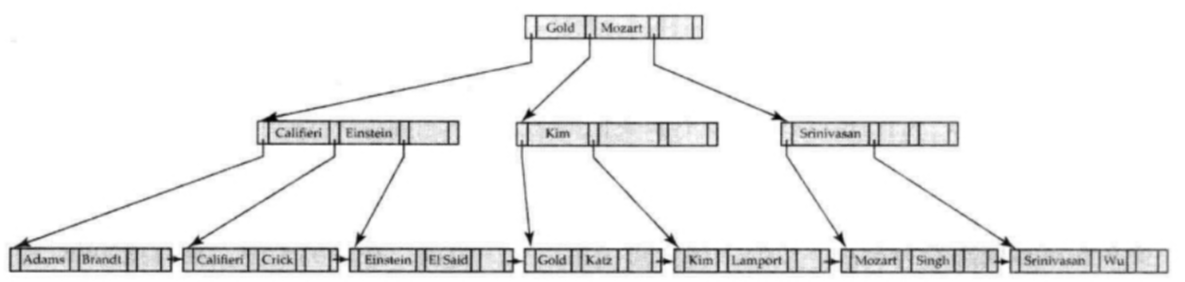
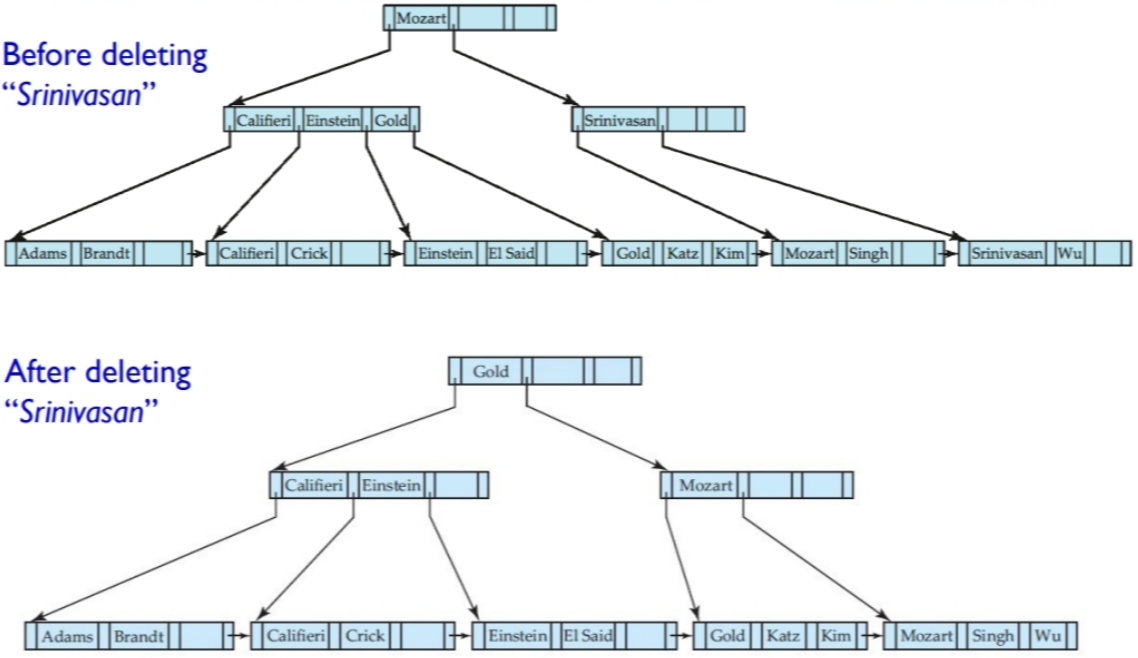
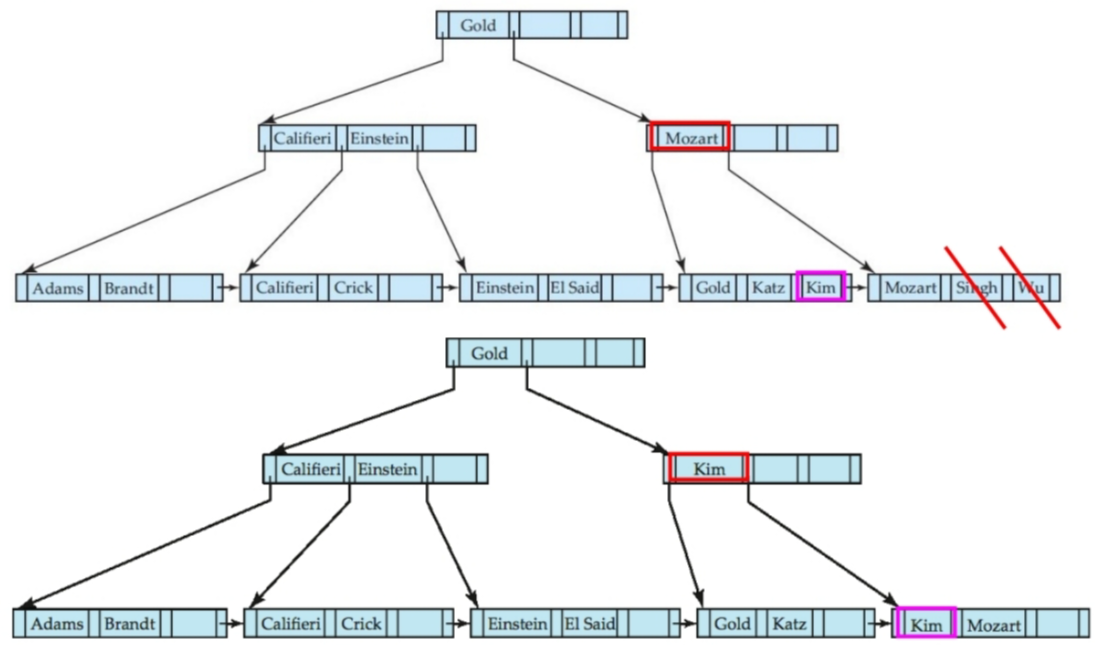
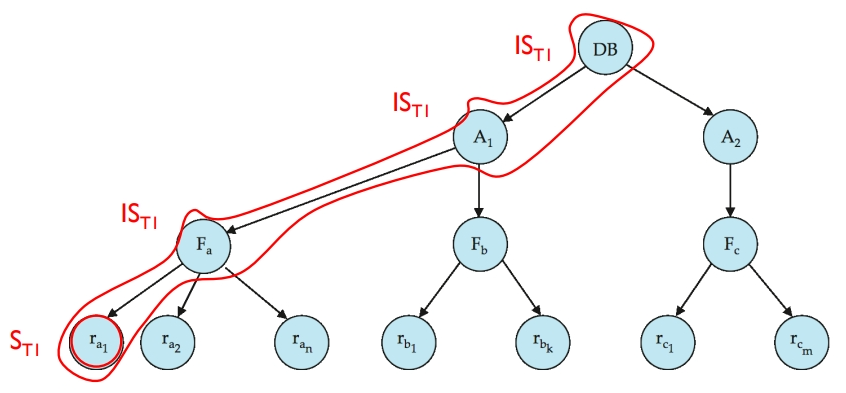
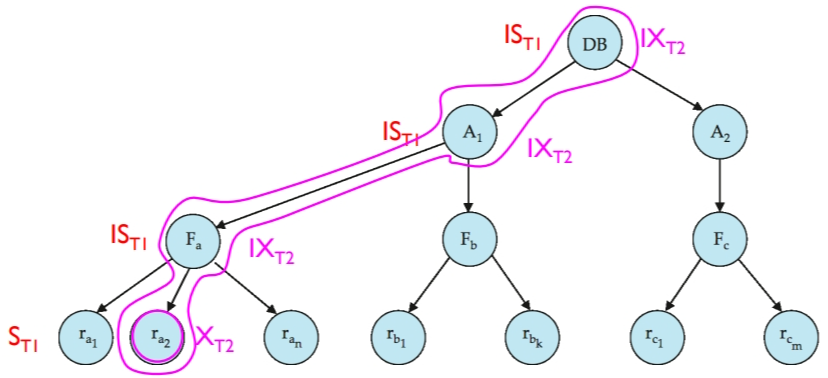
多粒度机制（Multiple granularity mechanism）允许数据项具有不同的大小，并定义一个数据粒度的层次结构，其中较小的粒度嵌套在较大的粒度之内。这样的层次结构可以用树状图形来表示。树中的每个节点都可以单独加锁。当一个事务显式地锁定树中的一个节点时，它隐式地以相同的模式锁定该节点的所有子孙节点。

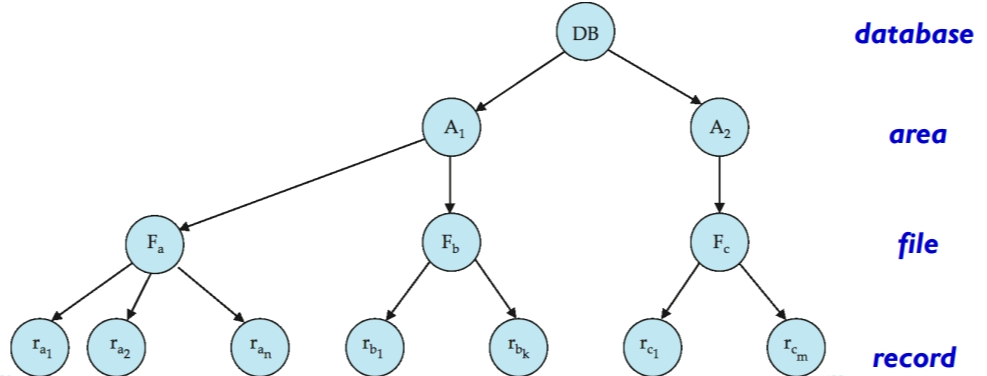
granularity

但是，每一次加锁，都需要判定当前节点是否能加锁。例如：事务 T1 想给 A1 加共享锁，但是系统必须检查 A1 的所有子节点中是否有排他锁。若有，则不能加锁。但如果每次加锁都需要搜索整个树，就违背了多粒度机制的初衷——快速地给大量数据加锁。

所以我们引入了一种新的锁的模式：意向锁（intention lock mode）。

意向锁

意向锁也是可能出现死锁的。

意向锁有五种锁的模式：

  • S（共享锁）
  • X（排他锁）
  • IS（共享意向锁）：表明将要在更低层次加共享锁。
  • IX（排他意向锁）：表明将要在更低层次加排他锁。
  • SIX（共享排他意向锁）：表明在更高层次加了共享锁，并且将要在更低层次加独占锁。（SIX = S + IX）

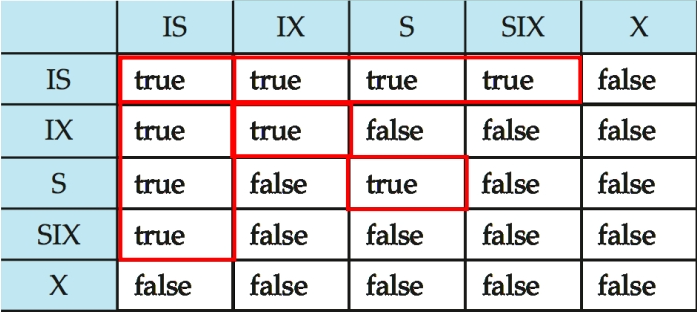
intention lock

核心想法就是：增加 IS、IX、SIX 模式，来反映子节点的上锁情况。这样给当前节点上锁时，就不必搜索当前节点的子树，检查当前节点的锁就能知道其子节点的上锁情况。当我们给一个节点上意向锁时，我们只需要更新当前节点和其父节点的锁即可，不需要更改其子节点的锁。

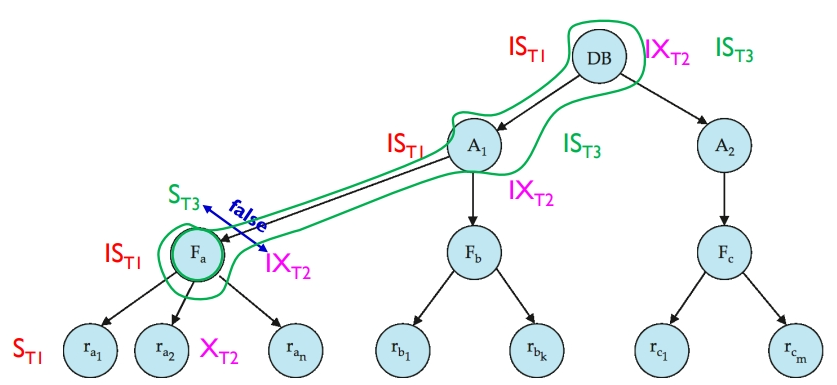
事务 Ti 可以使用以下规则锁定节点 Q：

  • 必须遵守上图种的锁兼容矩阵。
  • 必须首先锁定树的根节点，并且可以以任何模式锁定。
  • 事务 Ti 只有在 Q 的父节点被 Ti 以 IX 或 IS 模式锁定时，才能以 S 或 IS 模式锁定节点 Q。
  • 事务 Ti 只有在 Q 的父节点被 Ti 以 IX 或 SIX 模式锁定时，才能以 X、SIX 或 IX 模式锁定节点 Q。
  • 事务 Ti 只有在之前没有解锁过任何节点的情况下才能锁定节点（即：Ti 遵循二相锁协议）。
  • 事务 Ti 只有在 Q 的子节点都没有被 Ti 锁定的情况下才能解锁节点 Q。

请注意：锁定是从根到叶节点的顺序进行的，而解锁是从叶到根的顺序进行的。

举例说明一下，假设依次发生以下请求：

  • 事务 T1 读取记录 ra1 。

    example3.1

  • 事务 T2 更新记录 ra2 。

    example3.2

  • 事务 T3 读取文件 Fa 。（但此时 ST3  锁和 IXT2 锁相矛盾了，所以 T3 会进行等待）

    example3.3

时间戳

之前基于锁的各种协议，最终可序列化的顺序都是由上锁的时刻决定。现在我们介绍第二种实现并行控制的方法：基于时间戳的协议（Timestamp-Based Protocols）。这种方法的事务可序列化顺序是预先决定的。

事务时间戳

每个事务 Ti 都会被分配一个唯一的固定时间戳 TS(Ti)。这个时间戳在事务 Ti 开始执行之前由数据库系统分配。

  • 如果事务 Ti 被分配了时间戳 TS(Ti)，并且有一个新的事务 Tj 进入系统，那么 TS(Ti) < TS(Tj)。

  • 有两种简单的方法来实现时间戳方案：

    • 使用系统时钟的值作为时间戳——事务的时间戳等于事务进入系统时的时钟值。

    • 使用逻辑计数器，该计数器在分配新时间戳后递增——事务的时间戳等于事务进入系统时计数器的值。

时间戳决定了可串行化的顺序。

  • 如果 TS(Ti) < TS(Tj)，则生成度必须等效于一个串行调度，其中 Ti 出现在事务 Tj 之前。

数据时间戳

为了实现这个方案，协议为每个数据项 Q 维护两个时间戳值：

  • **W-timestamp(Q)**：成功执行写操作 write(Q) 的任意事务的最大时间戳。
  • **R-timestamp(Q)**：成功执行读操作 read(Q) 的任意事务的最大时间戳。

当新的指令（read(Q) 或 write(Q)）执行时，时间戳会被更新。

时间戳协议

时间戳排序协议确保：任何冲突的读写操作按照时间戳顺序执行。

假设事务 Ti 执行一个读操作 read(Q)：

  • 如果 TS(Ti) < W-timestamp(Q)，那么 Ti 需要读取一个已被后续事务覆盖的数据值。因此，读操作会被拒绝，并且 Ti 将被回滚。

  • 如果 TS(Ti) ≥ W-timestamp(Q)，则读操作会被执行，并且 R-timestamp(Q) 被设置为 R-timestamp(Q) 和 TS(Ti) 中的最大值。

假设事务 执行一个写操作 write(Q)：

  • 如果 TS(Ti) < R-timestamp(Q)，则表示 Ti 正想写一个已经被后续事务读取了的数据 Q 的值，但系统认为这个值不会再被产生。因此，写操作会被拒绝，并且 Ti 将被回滚。

  • 如果 TS(Ti) < W-timestamp(Q)，则表示 Ti 尝试写入一个已经过时的 Q 的值。因此，这个写操作也会被拒绝，并且 Ti 将被回滚。

  • 否则，写操作会被执行，并且设置 W-timestamp(Q) = TS(Ti)。

请注意：如果一个事务被回滚了，系统会重新给它分配一个时间戳，并重启它。

时间戳协议保证了所有事务按照时间戳的顺序执行完成。所以，在时间戳协议里，不会出现死锁。但是仍然可能出现饿死的情况：一系列短事务可能会不断的被重启，因为一些长事务一直在执行。

timestamp serializability

时间戳协议虽然避免了死锁的问题，但它不能避免级联，而且很可能不是可恢复的。

举例说明一下。假设事务 Ti 中止（abort），但是事务 Tj 已经读取了由 Ti 写入的数据项：

  • 那么事务 Tj 必须中止（abort）。如果允许 Tj 先提交，那么该调度就不是可恢复的。
  • 此外，任何已经读取了由 Tj 写入的数据项的事务都必须中止（abort）。
  • 这可能导致级联回滚，即一系列的事务被迫回滚。

这个问题的核心在于：当数据项 Q 在“被事务 Tj 写后”和“事务 Tj 提交”之间的时间里，数据项 Q 并不是盖棺定论的，可能因事务 Tj 的回滚而改变，但数据项 Q 又可能被其他事务读取。所以解决方法的核心也就是：让所有事务都等到数据盖棺定论的时候再读取。

常见解决方法有以下三种：

  • 在事务结束时一次性执行所有写操作。
  • 延迟读取未提交数据项，直到更新该数据项的事务已提交为止。
  • 跟踪未提交的写操作，只允许事务 Ti 在读取的值都是由已提交事务写入后才能提交（即提交依赖）。

Thomas 写规则

在时间戳协议的基础上，我们可以进一步增强数据库系统的并行能力。

考虑下图中的例子：事务 T27  因为 write(Q) 操作被迫回滚。但实际上，按照“事务 T27  先执行，事务 T28 后执行”的顺序，事务 T27 的 write(Q) 操作实际上会被事务 T28 的 write(Q) 操作覆盖掉。也就是说：事务 T27 的 write(Q) 操作根本没必要执行，事务 T27 也不必回滚。

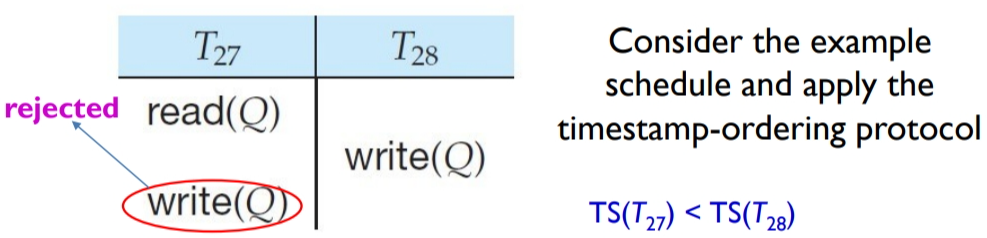
example4

对于过时的写操作，我们进行忽略。于是有了 Thomas’ Write Rule。

假设事务 Ti 发出写操作 write(Q)。

  1. 如果 TS(Ti) < R-timestamp(Q)：则表示 Ti 正在更新一个已经被后续事务读取了的 Q，而系统曾假定这个值不会再被产生。因此，系统拒绝写操作，并回滚事务 Ti。（与原协议相同）
  2. 如果 TS(Ti) < W-timestamp(Q)：则表示 Ti 尝试写入一个过时的 Q 的值。根据修改后的规则，这个写操作可以被忽略。（新规则）
  3. 否则：系统执行写操作，并将 W-timestamp(Q) 设置为 TS(Ti)。（与原协议相同）

（视图）可序列化

通过忽略过时的写操作，Thomas 的写入规则允许产生：不符合冲突可串行化但是正确的调度。这就促使我们定义一种新的可序列化：视图可串行化。

如果两个调度 S 和 S’ 包含相同的一组事务，并且满足以下三个条件，那么它们被称为视图等价。

第1、2条件保证了相同的值和计算。第2、3个条件保证了相同的最终状态。

  • 对于每个数据项 Q，如果事务 Ti 在调度 S 中读取了 Q 的初始值，则在调度 S’ 中，事务 Ti 也必须读取 Q 的初始值。（确保读取相同的初始值）
  • 对于每个数据项 Q，如果事务 Ti 在调度 S 中执行了 read(Q) 操作，并且这个值是由事务 Tj 执行的 write(Q) 操作产生的，则在调度 S’ 中，事务 Ti 也必须读取到由同一个事务 Tj 执行的 write(Q) 操作产生的值。（确保读取由同一事务写入的值）
  • 对于每个数据项 Q，在调度 S 中执行最终的 write(Q) 操作的事务（如果有的话），在调度 S’ 中也必须执行最终的 write(Q) 操作。（确保执行相同的最终写操作）

如果它与某个串行调度视图等价，调度 S 是视图可串行化（View Serializable）的。

View Serializability

发表于 更新于 分类于 Disqus：

引言

在实际场景中，数据库并不是完全可靠的。数据库可能在执行某些操作时崩了，导致一系列操作戛然而止。但有很多操作是必须一起执行的，比如银行转账，不能只执行从A账户扣钱，但不继续执行向B账户里加钱，这样会破坏数据一致性。

为了保证数据库在出现故障时，仍能保证数据的正确，我们引入了“事务”。

事务

A transaction is a unit of program execution that accesses and possibly updates various data items.

总的来说，事务（transaction）是一种机制，用来确保多个操作（如读取和写入数据）要么全部成功，要么全部失败，从而保持数据的一致性和完整性。事务中的所有操作作为一个整体，要么全部完成（提交），要么全部撤销（回滚），因此保证了数据在任何情况下都是一致的。

ACID性质

在数据库系统中，Transaction需要保持一下四个性质（ACID properties）：

  • 原子性（Atomicity）：事务中的操作，要么全部执行，要么全部没执行。
  • 一致性（Consistency）
  • 隔离性（Isolation）
  • 永久性（Durability）：事务成功完成后，即使系统出现故障，它对数据库所做的更改也会持久存在。

通俗地讲，一致性是指，在仅当前事务执行时（没有事务并发执行），数据库中的某些不变量要保持一致。比如银行转账时两个账户的余额之和要保持不变。（英文释义：If a transaction is run atomically in isolation starting from a consistent database, the database must again be consistent at the end of the transaction. ）

但是，像银行转账，先从A账户扣钱，再向B账户里转钱，必然有处于不一致状态的时候。执行一个事务时也是如此。我们必须保证：不一致状态是不可见的。这也是为什么要保证原子性——要么全做完，要么回退到全部没做，不能位于中间不一致状态。

consistency

原子性一般这样实现：数据库会记录一个事务对任何数据进行写操作前的旧值。 这些信息被写入一个称为日志（log）的文件中。如果事务没有完成其执行，数据库系统会从日志中恢复旧值，使其看起来像事务从未执行过一样。而且日志记录需要发生在事务开始修改数据库之前（log records need to be written to stable storage before any changes are made to the database on disk.）

诚然，事务序列运行（serially）是更容易实现的，但多个事务的并发运行能显著地提升性能，就像“一个人干活 Vs 一群人同时干活”：

  • 提升吞吐量和资源利用
  • 减少事务等待时间

但是，如果多个事务并发执行，它们的操作可能以某种不理想的方式交错进行，导致数据库处于不一致的状态。这就需要隔离性（保证隔离性才能实现并行控制）。

隔离性是指，多个事务可能并发执行，数据库要保证：

  • 对于任意两个事务 Ti 和 Tj 来说，Ti 看起来 要么是 Tj 在 Ti 开始之前就已经完成了执行，要么是 Tj 在 Ti 完成之后才开始执行。

从而实现，每个事务都不知道系统中同时执行的其他事务。

事务状态

为了跟准确地描述一个事务执行了多少，我们引入事务状态。

  • Active：初始状态，事务在执行过程中处于该状态。
  • Partially committed：在执行了最后一个语句之后，事务进入该状态。
  • Failed：在发现正常执行无法继续后，事务进入该状态。
  • Aborted：在事务被回滚（roll back）且数据库恢复到事务开始之前的状态后，事务进入中止状态。
  • Committed：在当前事务成功完成执行后，事务进入该状态。

states

特别地，我们需要小心：可观察的外部写操作（比如写入用户的屏幕，一旦发生，就不能撤销）。大多数系统允许这种写操作仅在事务进入Committed状态后才进行。

调度

调度（Schedule）是指一系列指令，并指定并发事务的指令在系统中执行的时间顺序。

且一个调度要满足：

  • 对于一组事务的调度必须包含这些事务中的所有指令。
  • 必须保持各个事务中指令的相对顺序（
  • 成功完成执行的事务，其最后一个语句将是commit指令。
  • 未成功完成执行的事务，其最后一个语句将是abort指令。

举一个例子：T1事务是从A转账50元到B，T2事务是A转账10%到B。下图的调度1是一个序列化的（serial）调度。

schedule1

可序列化

等价（equivalent）有很多种，因此对应的可序列化（Serializable）也有多种。这里我们指的都是冲突等价和冲突可序列化。

如果一个调度是等价于一个序列调度，则称为可序列化的（serializable）。所谓等价，通俗地讲，则是两个调度的最终结果相同。之后我们会给出严格定义。

下图中，调度3与调度1等价，是可序列化的调度。

schedule3

我们只关心read和write两类操作，特别是它们执行的先后顺序，忽略其他类型的操作。大多数时候出问题都是因为：最新值还未写入数据库，而另一事务已经提前读取或写入了数据。但需要指出的是：可能存在两个调度，它们产生相同的结果，但它们不是冲突等价的（相当于是“充分条件，但不必要”）。

我们考虑调度 S 中的两个连续的指令 I 、 J 。

如果 I 、 J 分别作用于不同的数据，那么它们的先后顺序不影响数据结果，怎么样都可以，不冲突。

如果 I 、 J 分别作用于同一个数据 Q ，那么有4种可能情况：

  • I = read(Q), J = read(Q)

  • I = read(Q), J = write(Q)

  • I = write(Q), J = read(Q)

  • I = write(Q), J = write(Q)

I 、 J 同时读取一个数据并不在意顺序，不冲突。但是 I 、 J 只要有至少一个是write操作，就会冲突（conflict），需要考虑其执行顺序。

从而我们可以严格的定义等价：

如果一个调度 S 可以通过一系列非冲突指令的交换转换为另一个调度 S’，我们称 S 和 S’ 是冲突等价（Conflict Equivalent）的。

可恢复性

Transaction Tj is dependent on Ti means that Tj has read data written by Ti .

到目前为止，我们都在假定事务不会失败的情况下讨论，但实际情况是事务失败总会发生。为了保证原子性，我们就必须撤销该事务的所有操作。但如果Ti 失败了，且 Tj 依赖于 Ti ，那么我们需要也将 Tj 撤销。

例如下图中，调度9中的T7使用了T6写入的A值，如果T6结果出问题，则T7结果也有问题。所以，T7依赖于T6 。

schedule9

可恢复调度（recoverable schedule）应当满足：

  • 如果一个事务 Tj 读取了之前由事务 Ti 写入的数据项，那么事务 Ti 将在事务 Tj 提交之前提交。

recoverable

可恢复性确保了：如果一个事务要用其他事务的数据项，则一定用的是最终数据，而不是过程中的数据。这样避免了一个数据出错导致一系列数据出错（级联效应）。

无级联的

像上面所所的，一个事务的失败可能触发一系列事务的回滚。这种情况称为级联回滚（cascading rollback）。这样的情况会大大降低数据库的性能。

所以我们希望调度是无级联的（cascadeless），亦即：

  • 任意一对事务 Ti 和 Tj ，如果一个事务 Tj 读取了之前由事务 Ti 写入的数据项，那么事务 Ti 将在事务 Tj 提交之前提交。

cascadeless

不难发现，无级联则可恢复。

发表于 更新于 分类于 Disqus：

引言

在数据库中，join 是经常使用的操作，但其工作量也可能是很大的。那么如何高效地完成 join 操作呢？

这篇 blog 将介绍：

  • 常见的 join 实现方式
  • 如何在 Postgresql 源代码中实现 block nested loop join

常见 join 算法

Simple Nested-Loop Join

简单来说，Simple Nested-Loop Join 就是一个双层 for 循环 ，通过循环外层表的行数据，逐个与内层表的所有行数据进行比较来获取结果。

用伪代码描述大致如下：

1
2
3
4
5
6
7
8
9
for (each tuple i in outer relation) {
	for (each tuple j in inner relation) {
        if (join_condition(tuple i, tuple j) is true)
      		emit (tuple i, tuple j)
       	else
      		continue
  }
}

特点：

Nested-Loop Join 简单粗暴容易理解，就是通过双层循环比较数据来获得结果，但是这种算法显然太过于粗鲁，如果每个表有1万条数据，那么对数据比较的次数=1万 * 1万 = 1亿次，很显然这种查询效率会非常慢。

当然，数据库肯定不会这么粗暴地 join，所以就出现了后面的两种对Nested-Loop Join 优化算法。在执行 join 查询时，数据库会根据情况选择后面的两种 join 优化算法的进行join查询。

Index Nested-Loop Join

Index Nested-Loop Join 的优化思路主要是：减少内层表数据的匹配次数。

简单来说，Index Nested-Loop Join 就是通过外层表匹配条件，直接与内层表索引进行匹配，避免和内层表的每条记录去进行比较，这样极大的减少了对内层表的匹配次数，从原来的 “匹配次数=外层表行数 * 内层表行数”，变成了 “外层表的行数 * 内层表索引的高度”，极大的提升了 join 的性能。

Index Nested-Loop Join

但是，Index Nested-Loop Join 算法的前提是：匹配的字段必须建立了索引。

Block Nested-Loop join

Block Nested-Loop Join 其优化思路是：减少内层表的扫表次数。

Block Nested-Loop Join 算法意在通过一次性缓存外层表的多条数据，以此来减少内层表的扫表次数，从而达到提升性能的目的。

Block Nested-Loop Join

如果无法使用 Index Nested-Loop Join 时候，一般都会使用 Block Nested-Loop Join 算法。

PostgreSQL 实验

准备工作

  1. 下载 postgresql 源代码：

    https://www.postgresql.org/ftp/source/v12.0/

  2. 在本地编译并安装 postgresql：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    # 切换到源代码目录
    cd postgresql-12.0

    # 初始化 make 配置
    /configure --enable-depend --enable-cassert --enable-debug CFLAGS="-O0" --prefix=$HOME/pgsql

    # 编译
    make

    # 安装(一般会安装到$HOME/pgsql)
    make install

  3. 初始化本地 postgresql 服务器：

    若你不幸把 pgsql 装到别的位置，把 $HOME/pgsql 替换成你安装的路径。

    1
    $HOME/pgsql/bin/initdb -D $HOME/pgsql/data --locale=C

  4. 启动 postgresql 服务器：

    1
    /home/[guanz]/pgsql/bin/pg_ctl -D /home/[guanz]/pgsql/data -l logfile start

  5. 连接 postgresql 服务器：

    1
    $HOME/pgsql/bin/psql postgres

  6. 关闭 postgresql 服务器：

    “Ctrl + D” 和 \q 均可以退出 postgresql 命令行。

    1
    2
    # This command depends on your installation location, please modify it
    /home/[guanz]/pgsql/bin/pg_ctl -D /home/[guanz]/pgsql/data stop

  7. 加载测试数据：

    1
    2
    3
    postgres=# CREATE DATABASE similarity;
    postgres-# \c similarity
    postgres-# \i /home/[guanz/data/]similarity_data.sql

    select_example

源代码解读

虽然源代码很多，但我们只关注以下几个文件：

  • src/backend/executor/nodeNestloop.c
  • src/include/executor/nodeNestloop.h
  • src/include/nodes/execnodes.h

Nested-Loop 主要算法都在 nodeNestloop.c 中实现：

其中 ExecNestLoop() 是执行嵌套循环连接，其余两个 ExecInitNestLoop() 和 ExecEndNestLoop() 则分别完成初始化和终止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
/*
* xht03：
* ExecNestLoop 是迭代器函数，不是一次执行完所有循环，
* 而是每次循环时执行一次的函数
*/
static TupleTableSlot *
ExecNestLoop(PlanState *pstate)
{
    /*
    * xht03：
    * node 指的是查询计划树中的一个节点。
    * 在这段代码中，NestLoopState *node 是
    * 一个指向 NestLoopState 结构体的指针，
    * 这个结构体通常包含了执行Nested Loop Join 所需要的状态信息。
    */
    NestLoopState *node = castNode(NestLoopState, pstate);
	NestLoop   *nl;
    
    /*
    * xht03：
    * Plan 指的是查询计划，
    * 它是数据库查询优化器生成的一种数据结构，
    * 用于描述如何执行一个SQL查询。
    * 查询计划是由一系列的操作步骤（或称为操作符）组成的树状结构，
    * 每一个操作步骤都对应查询计划树中的一个节点。
    */
	PlanState  *innerPlan;
	PlanState  *outerPlan;
    
    /*
    * xht03：
    * slot 意为“槽”
    * outerTupleSlot和innerTupleSlot是用来：
    * 存储从外部/内部关系（或称为左/右表）获取的当前元组
    */  
	TupleTableSlot *outerTupleSlot;
	TupleTableSlot *innerTupleSlot;
    
    // 连接条件
    // 其他条件（比如：where后面跟的表达式）
	ExprState  *joinqual;
	ExprState  *otherqual;
    
    // 存储执行过程中的上下文
	ExprContext *econtext;
	ListCell   *lc;
	
    // 检查中断（不用管）
	CHECK_FOR_INTERRUPTS();

	/*
	 * get information from the node
	 */
	ENL1_printf("getting info from node");

	nl = (NestLoop *) node->js.ps.plan;
	joinqual = node->js.joinqual;
	otherqual = node->js.ps.qual;
	outerPlan = outerPlanState(node);	// 记录外表所在的tuple
	innerPlan = innerPlanState(node);	// 记录内表所在的tuple
	econtext = node->js.ps.ps_ExprContext;

	/*
	 * Reset per-tuple memory context to free any expression evaluation
	 * storage allocated in the previous tuple cycle.
	 */
	ResetExprContext(econtext);

	/*
	 * Ok, everything is setup for the join so now loop until we return a
	 * qualifying join tuple.
	 */
	ENL1_printf("entering main loop");

	for (;;)
	{
		/*
		 * xht03:
		 * 当需要新的外部元组时，获取下一个的外部元组，
		 * 并让内表从头开始扫描（重置）
		 */
		if (node->nl_NeedNewOuter)
		{
			ENL1_printf("getting new outer tuple");
			outerTupleSlot = ExecProcNode(outerPlan);

			/*
			 * xht03：
			 * 如果下一个外部元组为空，则 join 完成了
			 */
			if (TupIsNull(outerTupleSlot))
			{
				ENL1_printf("no outer tuple, ending join");
				return NULL;
			}

			ENL1_printf("saving new outer tuple information");
			econtext->ecxt_outertuple = outerTupleSlot;
			node->nl_NeedNewOuter = false;
			node->nl_MatchedOuter = false;

			/*
			 * fetch the values of any outer Vars that must be passed to the
			 * inner scan, and store them in the appropriate PARAM_EXEC slots.
			 *
			 * xht03：
			 * 传递一些参数，不用管，也不要改
			 */
			foreach(lc, nl->nestParams)
			{
				NestLoopParam *nlp = (NestLoopParam *) lfirst(lc);
				int			paramno = nlp->paramno;
				ParamExecData *prm;

				prm = &(econtext->ecxt_param_exec_vals[paramno]);
				/* Param value should be an OUTER_VAR var */
				Assert(IsA(nlp->paramval, Var));
				Assert(nlp->paramval->varno == OUTER_VAR);
				Assert(nlp->paramval->varattno > 0);
				prm->value = slot_getattr(outerTupleSlot,
										  nlp->paramval->varattno,
										  &(prm->isnull));
				/* Flag parameter value as changed */
				innerPlan->chgParam = bms_add_member(innerPlan->chgParam,
													 paramno);
			}

			/*
			 * now rescan the inner plan
			 */
			ENL1_printf("rescanning inner plan");
			ExecReScan(innerPlan);
		}

		/*
		 * we have an outerTuple, try to get the next inner tuple.
		 */
		ENL1_printf("getting new inner tuple");

		innerTupleSlot = ExecProcNode(innerPlan);
		econtext->ecxt_innertuple = innerTupleSlot;

		if (TupIsNull(innerTupleSlot))
		{
			ENL1_printf("no inner tuple, need new outer tuple");

			node->nl_NeedNewOuter = true;

			if (!node->nl_MatchedOuter &&
				(node->js.jointype == JOIN_LEFT ||
				 node->js.jointype == JOIN_ANTI))
			{
				/*
				 * We are doing an outer join and there were no join matches
				 * for this outer tuple.  Generate a fake join tuple with
				 * nulls for the inner tuple, and return it if it passes the
				 * non-join quals.
				 * 
				 * xht03：
				 * 你可能也发现了：外部元组和内部元组的值，除了会存进 outerTupleSlot
				 * 和 innerTupleSlot，还要存进上下文 econtext 里。
				 * 这是因为：ExecQual() 判断是否满足等式条件的函数，是使用上下文中
				 * 存储的内外部元组信息进行判断的。
				 * 这样的函数还有很多，所以一定要记得更新上下文
				 */
				econtext->ecxt_innertuple = node->nl_NullInnerTupleSlot;

				ENL1_printf("testing qualification for outer-join tuple");
				
				if (otherqual == NULL || ExecQual(otherqual, econtext))
				{
					/*
					 * qualification was satisfied so we project and return
					 * the slot containing the result tuple using
					 * ExecProject().
					 */
					ENL1_printf("qualification succeeded, projecting tuple");
					return ExecProject(node->js.ps.ps_ProjInfo);
				}
				else
					InstrCountFiltered2(node, 1);
			}

			/*
			 * Otherwise just return to top of loop for a new outer tuple.
			 */
			continue;
		}

		/*
		 * at this point we have a new pair of inner and outer tuples so we
		 * test the inner and outer tuples to see if they satisfy the node's
		 * qualification.
		 *
		 * Only the joinquals determine MatchedOuter status, but all quals
		 * must pass to actually return the tuple.
		 */
		ENL1_printf("testing qualification");

		if (ExecQual(joinqual, econtext))
		{
			node->nl_MatchedOuter = true;

			/* In an antijoin, we never return a matched tuple */
			if (node->js.jointype == JOIN_ANTI)
			{
				node->nl_NeedNewOuter = true;
				continue;		/* return to top of loop */
			}

			/*
			 * If we only need to join to the first matching inner tuple, then
			 * consider returning this one, but after that continue with next
			 * outer tuple.
			 */
			if (node->js.single_match)
				node->nl_NeedNewOuter = true;

			if (otherqual == NULL || ExecQual(otherqual, econtext))
			{
				/*
				 * qualification was satisfied so we project and return the
				 * slot containing the result tuple using ExecProject().
				 */
				ENL1_printf("qualification succeeded, projecting tuple");

				return ExecProject(node->js.ps.ps_ProjInfo);
			}
			else
				InstrCountFiltered2(node, 1);
		}
		else
			InstrCountFiltered1(node, 1);

		/*
		 * Tuple fails qual, so free per-tuple memory and try again.
		 */
		ResetExprContext(econtext);

		ENL1_printf("qualification failed, looping");
	}
}

/* ----------------------------------------------------------------
 *		ExecInitNestLoop
 * ----------------------------------------------------------------
 */
NestLoopState *
ExecInitNestLoop(NestLoop *node, EState *estate, int eflags)
{
	NestLoopState *nlstate;

	/* check for unsupported flags */
	Assert(!(eflags & (EXEC_FLAG_BACKWARD | EXEC_FLAG_MARK)));

	NL1_printf("ExecInitNestLoop: %s\n",
			   "initializing node");

	/*
	 * create state structure
	 */
	nlstate = makeNode(NestLoopState);
	nlstate->js.ps.plan = (Plan *) node;
	nlstate->js.ps.state = estate;
	nlstate->js.ps.ExecProcNode = ExecNestLoop;

	/*
	 * Miscellaneous initialization
	 *
	 * create expression context for node
	 */
	ExecAssignExprContext(estate, &nlstate->js.ps);

	/*
	 * initialize child nodes
	 *
	 * If we have no parameters to pass into the inner rel from the outer,
	 * tell the inner child that cheap rescans would be good.  If we do have
	 * such parameters, then there is no point in REWIND support at all in the
	 * inner child, because it will always be rescanned with fresh parameter
	 * values.
	 */
	outerPlanState(nlstate) = ExecInitNode(outerPlan(node), estate, eflags);
	if (node->nestParams == NIL)
		eflags |= EXEC_FLAG_REWIND;
	else
		eflags &= ~EXEC_FLAG_REWIND;
	innerPlanState(nlstate) = ExecInitNode(innerPlan(node), estate, eflags);

	/*
	 * Initialize result slot, type and projection.
	 */
	ExecInitResultTupleSlotTL(&nlstate->js.ps, &TTSOpsVirtual);
	ExecAssignProjectionInfo(&nlstate->js.ps, NULL);

	/*
	 * initialize child expressions
	 */
	nlstate->js.ps.qual =
		ExecInitQual(node->join.plan.qual, (PlanState *) nlstate);
	nlstate->js.jointype = node->join.jointype;
	nlstate->js.joinqual =
		ExecInitQual(node->join.joinqual, (PlanState *) nlstate);

	/*
	 * detect whether we need only consider the first matching inner tuple
	 */
	nlstate->js.single_match = (node->join.inner_unique ||
								node->join.jointype == JOIN_SEMI);

	/* set up null tuples for outer joins, if needed */
	switch (node->join.jointype)
	{
		case JOIN_INNER:
		case JOIN_SEMI:
			break;
		case JOIN_LEFT:
		case JOIN_ANTI:
			nlstate->nl_NullInnerTupleSlot =
				ExecInitNullTupleSlot(estate,
									  ExecGetResultType(innerPlanState(nlstate)),
									  &TTSOpsVirtual);
			break;
		default:
			elog(ERROR, "unrecognized join type: %d",
				 (int) node->join.jointype);
	}

	/*
	 * finally, wipe the current outer tuple clean.
	 */
	nlstate->nl_NeedNewOuter = true;
	nlstate->nl_MatchedOuter = false;

	NL1_printf("ExecInitNestLoop: %s\n",
			   "node initialized");

	return nlstate;
}

/* ----------------------------------------------------------------
 *		ExecEndNestLoop
 *
 *		closes down scans and frees allocated storage
 * ----------------------------------------------------------------
 */
void
ExecEndNestLoop(NestLoopState *node)
{
	NL1_printf("ExecEndNestLoop: %s\n",
			   "ending node processing");

	/*
	 * Free the exprcontext
	 */
	ExecFreeExprContext(&node->js.ps);

	/*
	 * clean out the tuple table
	 */
	ExecClearTuple(node->js.ps.ps_ResultTupleSlot);

	/*
	 * close down subplans
	 */
	ExecEndNode(outerPlanState(node));
	ExecEndNode(innerPlanState(node));

	NL1_printf("ExecEndNestLoop: %s\n",
			   "node processing ended");
}

/* ----------------------------------------------------------------
 *		ExecReScanNestLoop
 * ----------------------------------------------------------------
 */
void
ExecReScanNestLoop(NestLoopState *node)
{
	PlanState  *outerPlan = outerPlanState(node);

	/*
	 * If outerPlan->chgParam is not null then plan will be automatically
	 * re-scanned by first ExecProcNode.
	 */
	if (outerPlan->chgParam == NULL)
		ExecReScan(outerPlan);

	/*
	 * innerPlan is re-scanned for each new outer tuple and MUST NOT be
	 * re-scanned from here or you'll get troubles from inner index scans when
	 * outer Vars are used as run-time keys...
	 */

	node->nl_NeedNewOuter = true;
	node->nl_MatchedOuter = false;
}

源代码修改

我们主要做了一下修改：

  • 新增了结构体类型 NestedBlock ，用于存放中间缓存的外部元组。

与之相应地：

  • 增加了 GetNestedBlock() 函数，用于获取新的中间元组。
  • 在上下文类型 ExprContext 中增加 NestedBlock 变量，将中间缓存元组记录在上下文中。
  • 修改 ExecNestLoop() 函数：外部元组一次取出至多 NESTED_BLOCK_SIZE 个元组放入缓存 NestedBlock 中，并照旧扫描内部元组。但每次需要将缓存中的所有 outer tuple 一一与 inner tuple 进行比较，且外部元组的指针需要往后移动 NESTED_BLOCK_SIZE 个元组。

修改细节如下（修改之处都加有 xht03 注释）：

execnodes.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// xht03
#define NESTED_BLOCK_SIZE 64

typedef struct NestedBlock{
    TupleTableSlot *tuple[NESTED_BLOCK_SIZE];	// 存放外部元组
	bool isMatched[NESTED_BLOCK_SIZE];			// 是否在内部关系中匹配到过
    int size;									// 缓存中的元组个数
} NestedBlock;


typedef struct ExprContext
{
	NodeTag		type;

	/* Tuples that Var nodes in expression may refer to */
#define FIELDNO_EXPRCONTEXT_SCANTUPLE 1
	TupleTableSlot *ecxt_scantuple;
#define FIELDNO_EXPRCONTEXT_INNERTUPLE 2
	TupleTableSlot *ecxt_innertuple;
#define FIELDNO_EXPRCONTEXT_OUTERTUPLE 3
	TupleTableSlot *ecxt_outertuple;

// xht03
	NestedBlock *ecxt_block;

	/* Memory contexts for expression evaluation --- see notes above */
	MemoryContext ecxt_per_query_memory;
	MemoryContext ecxt_per_tuple_memory;

	/* Values to substitute for Param nodes in expression */
	ParamExecData *ecxt_param_exec_vals;	/* for PARAM_EXEC params */
	ParamListInfo ecxt_param_list_info; /* for other param types */

	/*
	 * Values to substitute for Aggref nodes in the expressions of an Agg
	 * node, or for WindowFunc nodes within a WindowAgg node.
	 */
#define FIELDNO_EXPRCONTEXT_AGGVALUES 8
	Datum	   *ecxt_aggvalues; /* precomputed values for aggs/windowfuncs */
#define FIELDNO_EXPRCONTEXT_AGGNULLS 9
	bool	   *ecxt_aggnulls;	/* null flags for aggs/windowfuncs */

	/* Value to substitute for CaseTestExpr nodes in expression */
#define FIELDNO_EXPRCONTEXT_CASEDATUM 10
	Datum		caseValue_datum;
#define FIELDNO_EXPRCONTEXT_CASENULL 11
	bool		caseValue_isNull;

	/* Value to substitute for CoerceToDomainValue nodes in expression */
#define FIELDNO_EXPRCONTEXT_DOMAINDATUM 12
	Datum		domainValue_datum;
#define FIELDNO_EXPRCONTEXT_DOMAINNULL 13
	bool		domainValue_isNull;

	/* Link to containing EState (NULL if a standalone ExprContext) */
	struct EState *ecxt_estate;

	/* Functions to call back when ExprContext is shut down or rescanned */
	ExprContext_CB *ecxt_callbacks;
} ExprContext;

nodeNestloop.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#ifndef NODENESTLOOP_H
#define NODENESTLOOP_H

#include "nodes/execnodes.h"


// xht03
extern void *GetNestedBlock(NestedBlock *block, PlanState *outerPlan);


extern NestLoopState *ExecInitNestLoop(NestLoop *node, EState *estate, int eflags);
extern void ExecEndNestLoop(NestLoopState *node);
extern void ExecReScanNestLoop(NestLoopState *node);

#endif							/* NODENESTLOOP_H */

nodeNestloop.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
// xht03
void *GetNestedBlock(NestedBlock *block, PlanState *outerPlan)
{
    for(int i = 0; i < NESTED_BLOCK_SIZE; i++)
    {
        block->tuple[i] = ExecProcNode(outerPlan);
		block->isMatched[i] = false;
        if(TupIsNull(block->tuple[i]))
        {
            block->size = i;
            break;
        }
    }
}



static TupleTableSlot *
ExecNestLoop(PlanState *pstate)	
{
	NestLoopState *node = castNode(NestLoopState, pstate);
	NestLoop   *nl;
	PlanState  *innerPlan;
	PlanState  *outerPlan;
	TupleTableSlot *outerTupleSlot;
	TupleTableSlot *innerTupleSlot;
	ExprState  *joinqual;
	ExprState  *otherqual;
	ExprContext *econtext;
	ListCell   *lc;

	// xht03
	NestedBlock block;


	CHECK_FOR_INTERRUPTS();	


	/*
	 * get information from the node
	 */
	ENL1_printf("getting info from node");

	nl = (NestLoop *) node->js.ps.plan;
	joinqual = node->js.joinqual;
	otherqual = node->js.ps.qual;
	outerPlan = outerPlanState(node);
	innerPlan = innerPlanState(node);
	econtext = node->js.ps.ps_ExprContext;

	/*
	 * Reset per-tuple memory context to free any expression evaluation
	 * storage allocated in the previous tuple cycle.
	 */
	ResetExprContext(econtext);

	/*
	 * Ok, everything is setup for the join so now loop until we return a
	 * qualifying join tuple.
	 */
	ENL1_printf("entering main loop");

	for (;;)
	{
		/*
		 * If we don't have an outer tuple, get the next one and reset the
		 * inner scan.
		 */
		if (node->nl_NeedNewOuter)
		{
			ENL1_printf("getting new outer tuple");
			// xht03
			GetNestedBlock(&block, outerPlan);


			/*
		 	 * if there are no more outer tuples, then the join is complete..
			 */
			// xht03
			if (block.size == 0)
			{
				ENL1_printf("no outer tuple, ending join");
				return NULL;
			}

			ENL1_printf("saving new outer tuple information");
			//econtext->ecxt_outertuple = outerTupleSlot;	// 记录外表所在的tuple，更新上下文
			
			// xht03
			outerTupleSlot = block.tuple[block.size - 1];
			econtext->ecxt_outertuple = outerTupleSlot;
			econtext->ecxt_block = &block;
			node->nl_NeedNewOuter = false;
			node->nl_MatchedOuter = false;
            
			/*
			 * fetch the values of any outer Vars that must be passed to the
			 * inner scan, and store them in the appropriate PARAM_EXEC slots.
			 */
            // 将外表的一些参数传递给内表
			foreach(lc, nl->nestParams)
			{
				NestLoopParam *nlp = (NestLoopParam *) lfirst(lc);
				int			paramno = nlp->paramno;
				ParamExecData *prm;
				prm = &(econtext->ecxt_param_exec_vals[paramno]);
				/* Param value should be an OUTER_VAR var */
				Assert(IsA(nlp->paramval, Var));
				Assert(nlp->paramval->varno == OUTER_VAR);
				Assert(nlp->paramval->varattno > 0);
				prm->value = slot_getattr(outerTupleSlot,
										  nlp->paramval->varattno,
										  &(prm->isnull));
				/* Flag parameter value as changed */
				innerPlan->chgParam = bms_add_member(innerPlan->chgParam,
													 paramno);
			}
			/*
			 * now rescan the inner plan
			 */
            // 重新确定内表从哪里开始扫描
			ENL1_printf("rescanning inner plan");
			ExecReScan(innerPlan);
		}


		/*
		 * we have an outerTuple, try to get the next inner tuple.
		 */
		ENL1_printf("getting new inner tuple");
		innerTupleSlot = ExecProcNode(innerPlan);		// 获取新的内部节点（tuple）
		econtext->ecxt_innertuple = innerTupleSlot;		// 记录内表所在的tuple，更新上下文

		if (TupIsNull(innerTupleSlot))
		{
			ENL1_printf("no inner tuple, need new outer tuple");
			node->nl_NeedNewOuter = true;
			/*
			* xht03:
			* If not all the tuples in the block have been matched,
			* or the join type is left-join or anti-join
			*/
			if (!node->nl_MatchedOuter &&
				(node->js.jointype == JOIN_LEFT ||
				 node->js.jointype == JOIN_ANTI))
			{
				/*
				 * We are doing an outer join and there were no join matches
				 * for this outer tuple.  Generate a fake join tuple with
				 * nulls for the inner tuple, and return it if it passes the
				 * non-join quals.
				 */

				for(int i = 0; i < block.size; i++){
					econtext->ecxt_outertuple = block.tuple[i];
					if(!block.isMatched[i]){
                        // set to a empty tuple
						econtext->ecxt_innertuple = node->nl_NullInnerTupleSlot;
                        
                        // 检查非连接条件（non-join quals）的其他条件是否满足
						ENL1_printf("testing qualification for outer-join tuple");
						if (otherqual == NULL || ExecQual(otherqual, econtext))
						{
							/*
						 	* qualification was satisfied so we project and return
						 	* the slot containing the result tuple using
						 	* ExecProject().
						 	*/
							ENL1_printf("qualification succeeded, projecting tuple");
							return ExecProject(node->js.ps.ps_ProjInfo);
						}
						else
							InstrCountFiltered2(node, 1);
					}
				}
			}
			/*
			 * Otherwise just return to top of loop for a new outer tuple.
			 */
			continue;
		}
		/*
		 * at this point we have a new pair of inner and outer tuples so we
		 * test the inner and outer tuples to see if they satisfy the node's
		 * qualification.
		 *
		 * Only the joinquals determine MatchedOuter status, but all quals
		 * must pass to actually return the tuple.
		 */
		ENL1_printf("testing qualification");
		
		// 测试是否满足 join 条件
		// xht03
		int matched_num = 0;

		for(int i = 0; i < block.size; i++){
			econtext->ecxt_outertuple = block.tuple[i];
			if (ExecQual(joinqual, econtext))
			{
				//xht03
				if(!block.isMatched[i]){
					matched_num++;
					block.isMatched[i] = true;
				}

				/*
				* If we only need to join to the first matching inner tuple, then
				* consider returning this one, but after that continue with next
				* outer tuple.
				*/
			
				if (otherqual == NULL || ExecQual(otherqual, econtext))
				{
					/*
					* qualification was satisfied so we project and return the
					* slot containing the result tuple using ExecProject().
					*/
					ENL1_printf("qualification succeeded, projecting tuple");
					return ExecProject(node->js.ps.ps_ProjInfo);
				}
				else
					InstrCountFiltered2(node, 1);
			}
			else
				InstrCountFiltered1(node, 1);
		}
		/*
		* xht03:
		* If all tuples in the block have been matched
		*/
		if(matched_num == block.size)
		{
			node->nl_MatchedOuter = true;
			/* In an antijoin, we never return a matched tuple */
			if (node->js.jointype == JOIN_ANTI || node->js.single_match)
			{
				node->nl_NeedNewOuter = true;
			}	
		}

			
		/*
		 * Tuple fails qual, so free per-tuple memory and try again.
		 */
		ResetExprContext(econtext);
		ENL1_printf("qualification failed, looping");
	}
}

源代码测试

重新编译并安装 postgresql 后，设置 NESTED_BLOCK_SIZE = 1、2、8、64、128、1024，运行下面语句两次，取第二次运行时间。

在数据库命令行中输入：\timing，打开测时间功能。

1
SELECT count(*) FROM restaurantaddress ra, restaurantphone rp WHERE ra.name = rp.name;

Timing

NESTED_BLOCK_SIZE 时间1/ms 时间2/ms 时间3/ms
1 2.710 2.559 2.565
2 2.579 2.753 2.636
8 2.337 2.483 2.716
64 2.277 2.441 1.896
128 2.657 2.543 2.464
1024 2.871 2.743 2.778

这样的实验结果是符合预期的：

  • NESTED_BLOCK_SIZE 太小时，与 Simple Nested-Loop 相近；当 NESTED_BLOCK_SIZE 太大时，就相当于内外表互换后的 Simple Nested-Loop。所以当 NESTED_BLOCK_SIZE 取一个大小适中的值时，Block Nested-Loop 才能性能最大化。

发表于 分类于 Disqus：

基本结构

添加注释快捷键：ctrl + /

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
<!-- DOCTYPE：告诉浏览器我们使用什么规范，省略亦可 -->
<!-- 写在html标签里的内容才会显示 -->
<!DOCTYPE html>
<html>
<head>
    <!-- meta：描述性标签，描述网页的一些信息，一般用来做SEO（搜索引擎优化） -->
    <meta charset="UTF-8">
    <meta name="keyword" content="HTML example">
    <meta name="description" content="This is an example of HTML">
    <title>我的第一个HTML页面</title>
</head>
<body>
    <h1>欢迎来到我的网页</h1>
    <p>Hello World!</p>
    <p>这是一个简单的HTML页面。</p>
</body>
</html>
  • <html>称为开放标签，</html>称为闭合标签。
  • <meta> charset="UTF-8"称为自闭合标签。
  • title是指浏览器顶部页眉方框所显示的，并不是页面内的标题。

hello world

标签

输入p并按tab键，会自动生成<p></p>标签。其余类似。

基本标签

  • <h1></h1>：标题
  • <p></p>：段落
  • <hr>或<hr/>：水平线
  • <br>：换行
  • <b></b>或<strong></strong>：粗体
  • <i></i>或<em></em>：斜体
  • &...;：转义字符（&表示转义）
  • &nbsp;：空格
  • <img src="" alt="">：图像
  1. 空格键无论多少，都视为一个空格。多空格需用转义字符&nbsp。
  2. 图像引用中src和alt必不可少。其余字段可以添加或省略。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
<!DOCTYPE html>
<html>
<head>
    <meta charset="UTF-8">
    <title>基本标签</title>
</head>
<body>
    <!-- 标题标签 -->
    <h1>欢迎来到我的网页</h1>
    <h2>一首小诗</h2>
    <!-- 段落标签 -->
    <p>Do not go gentle into that good night</p>
    <p>Old age should burn and rave at close of day</p>
    <p>Rage, rage against the dying of the light</p>
    <!-- 水平线 -->
    <hr>
    <!-- 换行 -->
    两只老虎	两只老虎	跑得快 <br>
    一只没有眼睛	一直没有尾巴 <br>
    真奇怪		真奇怪 <br>
    <!-- 粗体与斜体 -->
    <b> I love you. </b>
    <strong> I love you. </strong>
    <i> I miss you. </i>
    <em> I miss you. </em>
    <!-- 特殊符号 -->
    &copy; 版权归延绪所有（版权符号） <br>
    &lt; &gt; &amp; &quot; &nbsp;（小于、大于、与、引号、空格） <br>
    空&nbsp;&nbsp;&nbsp;格 <br>
    <!-- 图像标签 -->
    <img src="../resources/images/SummerGhost3.png" alt="替代文字" title="悬停文字" width="960" height="540">
</body>
</html>

tags

超链接标签