延绪的水上书
0%

二叉搜索树

发表于 更新于 分类于 Disqus：

二叉搜索树

二叉搜索树（Binary Search Tree，BST）是一种特殊的二叉树，它具有以下性质：

  • 有序性：对于树中的任意节点，其左子树上所有节点的值都小于该节点的值，其右子树上所有节点的值都大于该节点的值。

  • 二叉树结构：每个节点最多有两个子节点，即左子节点和右子节点。

  • 没有键值重复：树中不存在两个节点具有相同的键值。

二叉搜索树的基本操作包括：

  • 查找（Search）：给定一个值，查找树中是否存在该值。
  • 插入（Insert）：插入一个新的值。
  • 删除（Delete）：删除树中的一个节点。
  • 遍历（Walk）：二叉搜索树可以通过中序遍历得到一个有序的元素序列。

二叉搜索树上的基本操作所花费的时间与这棵树的高度 h 成正比。

遍历操作

二叉搜索树性质允许我们通过一个简单的递归算法来按序输出二叉搜索树中的所有关键字，这种算法称为中序遍历（inorder tree walk）算法。

这样命名的原因是输出的子树根的关键字位于其左子树的关键字值和右子树的关键字值之间。（前序遍历、后序遍历类似。）

伪代码如下：

1
2
3
4
5
INORDER-TREE-WALK(x)
	if x != NIL
    	INORDER-TREE-WALK(x.left)
        print x.key
        INORDER-TREE-WALK(x.right)

显然，遍历一个二叉搜索树的时间代价是 **Θ(n)**。

查询操作

在一棵高度为h 的二叉搜索树上，查询操作 SEARCH、MINIMUM、MAXIMUM、SUCCESSOR 和 PREDECESSOR 均可以在 O(h) 时间内完成。

查找

我们通过 TREE-SEARCH(x, k)，查找以x为根的树中是否包含关键字 k。

1
2
3
4
5
6
7
8
TREE-SEARCH(x, k)
	if x==NIL or k==x.key
		return x

	if k < x.key
		return TREE-SEARCH(x.left, k)

	else return TREE-SEARCH(x.right, k)

不难证明，查找操作的时间代价是 **O(h)**。

最小值和最大值

TREE-MINIMUM(x)寻找以x为根的树中的最小值（就是子树的最左节点）。

1
2
3
4
TREE-MINIMUM(x)
	while x.left != NIL
		x = x.left
	return x

TREE-MAXIMUM(x)寻找以x为根的树中的最大值（就是子树的最右节点）。

1
2
3
4
TREE-MAXIMUM(x)
	while x.right != NIL
		x = x.right
	return x

这两个过程在一棵高度为 h 的树上均能在 O(h) 时间内执行完。

后继和前驱

所谓后继，就是当前节点在中序遍历过程中的下一个节点。这也是从小到大排序中，大于当前节点的最小节点。

前驱同理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# python 实现
# 寻找后继步骤：
# 1. 如果有右子树，后继是右子树中的最小节点
# 2. 如果没有，后继是当前节点的某个祖先节点

def find_successor(node):
    # 如果有右子树
    if node.right:
        return find_min(node.right)
    
    # 如果没有右子树
    parent = node.parent
    while parent and node == parent.right:
        node = parent
        parent = parent.parent
    return parent


def find_min(node):
    while node.left:
        node = node.left
    return node
1
2
3
4
5
6
7
# python 实现
# 二叉树节点定义
class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

该过程或者遵从一条简单路径沿树向上或者遵从简单路径沿树向下。所以，SUCCESSOR 操作可以在 O(h) 时间内完成。

插入操作

插入操作，与查找操作类似，只不过是在二叉搜索树中没能找到对应元素。此时，我们就在查找路径的尽头，插入新元素。

所以，TREE-INSERT 操作可以在 O(h) 时间内完成。

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
TREE-INSERT(T, z)
	y = NIL
	x = T.root

	while x != NIL
		y = x
		if z.key < x.key
			x = x.left
		else
			x = x.right

	z.parent = y

	if y == NIL
		T.root = z  
	else if z.key < y.key
	    y.left = z
	else
	    y.right = z

删除操作

删除的过程如下：

  • 如果被删除节点 z 没有孩子，则直接删除 z。
  • 如果 z 只有一个孩子，那么 z 孩子替代 z 的位置。
  • 如果 z 有两个孩子：
    • z 的后继 y（一定在 z 的右子树中）替代 z 的位置。
    • y 的孩子代替 y 的位置。（y 是子树中的最左节点，只有一个孩子。）

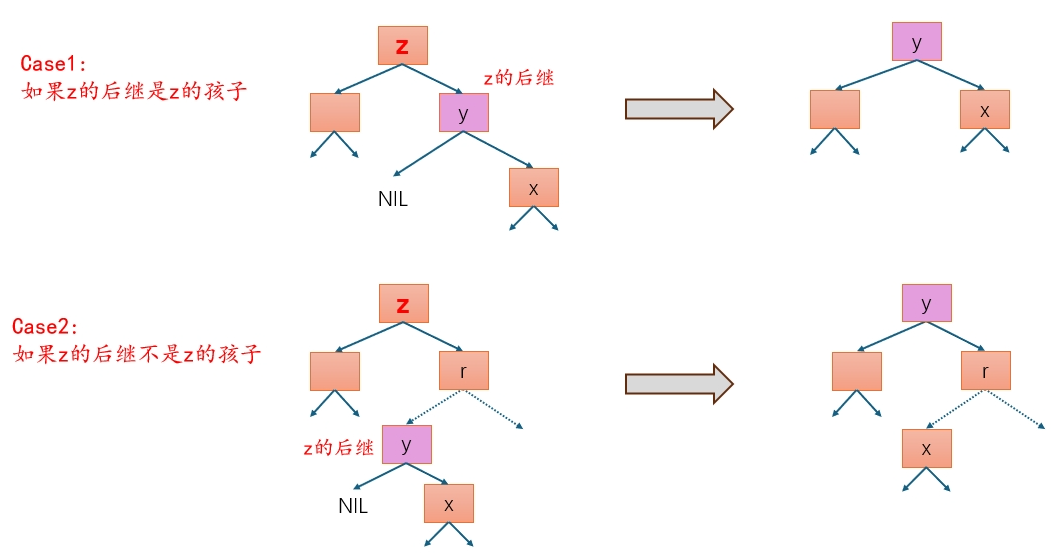
不难证明，TREE-DELETE 能在 O(h) 时间内完成。

随机构建

随机构建二叉搜索树是指：按随机次序插入关键字到一棵初始的空树中而生成的树，且输入的关键字排列等可能的出现。

一棵有 n 个不同关键字的随机构建二叉搜索树的期望高度为 **O(lgn)**。

证明：