延绪的水上书
0%

散列表

发表于 更新于 分类于 Disqus：

散列表

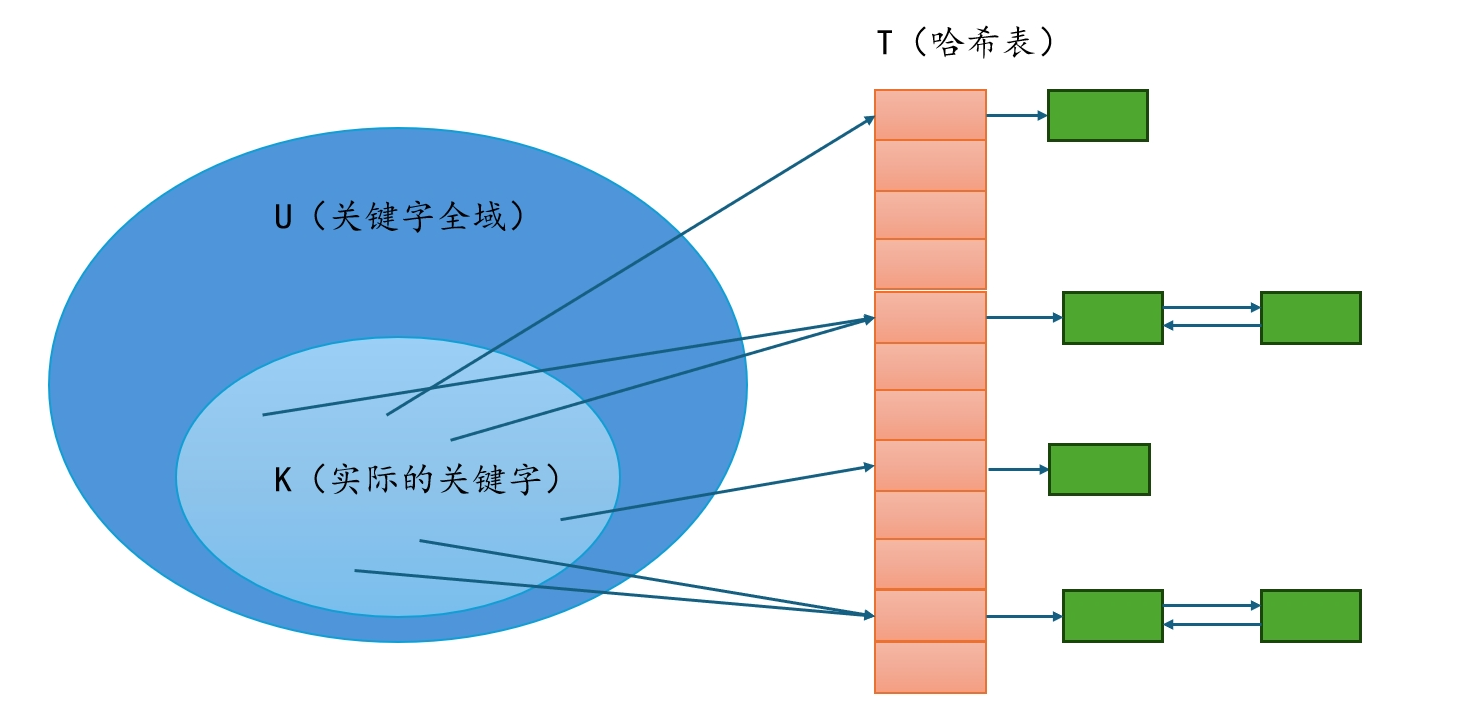
散列表（Hash Table），也称为哈希表，是一种通过哈希函数将键（Key）映射到表中一个位置以便快速访问记录的数据结构。它的主要目的是提供快速的数据插入、删除和查找操作。散列表通常由数组支持，这个数组称为“槽”或“桶”，数组的每个位置对应一个可能的哈希值。

大量键值对存储时：

  • 如果使用数组，并使用键作为索引，则当键的取值范围很广，但键值对数量却不多时：需要开辟很大的数组空间，却只有很少数空间被使用，造成空间浪费。
  • 所以，我们希望通过hash function将原本稀疏散落在数组各处的键值对，通过函数映射，集中存放在一个更小的空间中，提高空间利用率。

散列表的基本操作包括：

  1. 插入（Insert）：将一个新的键值对插入到散列表中。
  2. 查找（Search）：通过给定的键快速找到对应的值。
  3. 删除（Delete）：从散列表中删除一个键值对。

散列表的工作原理如下：

  1. 哈希函数（Hash Function）：选择一个合适的哈希函数，它能够将输入的键（可以是任意数据类型）转换为数组索引。一个好的哈希函数应该能够均匀地将键分布在数组的索引上，以减少冲突。
  2. 冲突解决（Collision Resolution）：由于不同的键可能会映射到同一个索引上，这种情况称为冲突。解决冲突的方法有：
    • 链地址法（Chaining）：每个数组索引处都有一个链表，所有映射到该索引的键值对都存储在这个链表中。
    • 开放寻址法（Open Addressing）：如果发生冲突，寻找表中的另一个空闲位置来存储该键值对。常见的开放寻址策略有线性探测、二次探测和双重散列。

冲突解决

链地址法

在链地址法（chaining）中，每个数组索引（或称为“槽”或“桶”）都关联一个链表，所有映射到该索引的元素都会被存储在这个链表中。

链地址法

链地址法的插入、查找、删除操作的伪代码如下：

1
2
3
4
5
6
7
8
CHAINED-HASH-INSERT(T ,x)
	insert x at the head of list T[h(x. key)]

CHAINED-HASH-SEARCH(T,k)
	search for an element with key in list T[h(k)]

CHAINED-HASH-DELETE(T,x)
	delete x from the list T[h(x.key)]

给定一个能存放 n 个元素的、具有 m 个槽位的散列表 T。定义 T 的装载因子（load factor） α 为n/m，即：一个链的平均存储元素数。

  • 插入操作：将新的元素链接到对应链表的头部，用时**O(1)**。

  • 删除操作：**如果是双向链表，用时O(1)**。如果是单向链表，用时与搜索操作时间相近。

    注意，这里删除操作CHAINED-HASH-DELETE(T,x)以元素 x 而不是它的关键字 k 作为输入，所以无需先搜索 x。

  • 搜索操作：

    在简单均匀散列的假设下，对于用链接法解决冲突的散列表，一次不成功查找的平均时间为 Θ(1 + α) 。

    证明：如果查找的关键字 k 不在哈希表中，则需要首先找到对应槽的链表，再遍历整个链表，确定关键字 k 不在哈希表中。而链表的长度期望是 α 。所以总用时是：Θ(1 + α) 。

    在简单均匀散列的假设下，对于用链接法解决冲突的散列表，一次成功查找所需的平均时间为 Θ(1 + α) 。

    证明：如果查找的关键字 k 在哈希表中，则需要先找到对应槽的链表，再搜索该链表。链表期望长度是 α ，关键字 k 等可能地出现在链表第1、2、……、α 个位置。所以总用时是：Θ(1 + (1+α)/2) = Θ(1 + α) 。

综上，当n、m数量级相近时，即n=O(m)时：链地址法的所有字典操作均是 O(1) 时间。

python代码实现大致如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 双向链表
class DLLNode:
    def __init__(self, key, value):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None

# 哈希表
class HashTable:
    def __init__(self, size=10):
        self.size = size
        self.table = [None] * self.size

    def _hash(self, key):
        return hash(key) % self.size

开放寻址法

在开放寻址法(open addressing) 中，所有的元素都存放在散列表里。这里既没有链表，也没有元素存放在散列表外。因此在开放寻址法中，散列表可能会被填满，且装载因子 α 不超过1。

插入操作

两个不同的键被哈希函数映射到同一个索引时，开放寻址法会再寻找新的空位索引，直至找到，再存放新插入的键值对。

插入操作伪代码如下：

HASH-INSERT(T,x)将元素 x 插入到哈希表 T 中。

如果第一次 hash 后的位置冲突了，则会再做第2、3……次 hash，直至找到空位用以插入新元素。所以**开放寻址法的 hash 函数需要两个参数：关键字 k 和第几次 i **。

1
2
3
4
5
6
7
8
9
10
HASH-INSERT(T,x)
	i=0
	repeat
		j=h(x.key,i)
		if T[j]==NIL
			T[j]=x
			return j
		else i=i+1
	until i==m
	error "hash table overflow"

常见探查方法，也即是对应的哈希函数有：

  • 线性探查：

    当发生冲突时，通过按顺序查找下一个空闲位置来存储键值对。

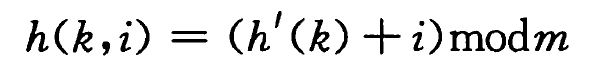
    i=0、1、……、m-1

    线性探查方法比较容易实现，但它存在着一个问题（群集现象）：

    当一个空槽前有 i 个满的槽时，该空槽为下一个将被占用的概率是 (i+1)/m。连续被占用的槽就会变得越来越长，因而平均查找时间也会越来越大。

    随着连续被占用的槽不断增加，平均查找时间也随之不断增加。

  • 二次探查：

    为了减轻线性探查的群集现象，我们每次往后推移二次函数个位置，进行探查。

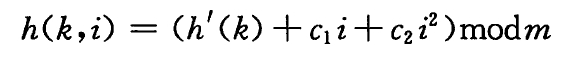
  • 双重散列：

    双重散列通过两个不同的哈希函数来计算候选位置。

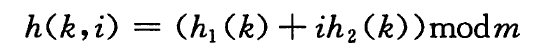
查找操作

查找操作与插入操作类似。

查找操作伪代码如下：

1
2
3
4
5
6
7
8
9
HASH_SEARCH(T,k)
	i=0
	repeat
		j=h(k,j)
		if T[j]==k
			return j
		i=i+1
	until T[j]==NIL or i==m
	return NIL
删除操作

采用开放寻址法时，删除操作是难以实现的。

例如：在插入关键字 k 时，发现槽 i 被占用了，则 k 就被插入到后面的位置上。此时我们欲将槽 i 中的关键字删除，那么就无法检索到关键字 k 了。

所以，删除操作不能直接删除，置为NIL，而是：删除后需要将槽标记为DELETED。

为此，在必须具备删除操作的情形下，一般不采用开放寻址法，而采用链地址法。

算法分析

给定一个装载因子为 α=n/m < 1 的开放寻址散列表，并假设是均匀散列的，则对于一次不成功的查找，其期望的探查次数至多为 1/(1 - α) 。

证明：

对于一个不成功的探查，我们假设经历了 X 次探查。

对于第 i 次探查，如果是空位，则我们知道散列表中没有该关键字，否则还需要继续探查。

现在有 n 个元素和 m 个槽。

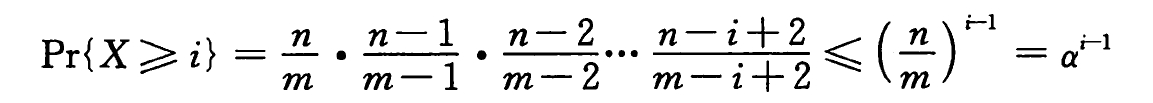
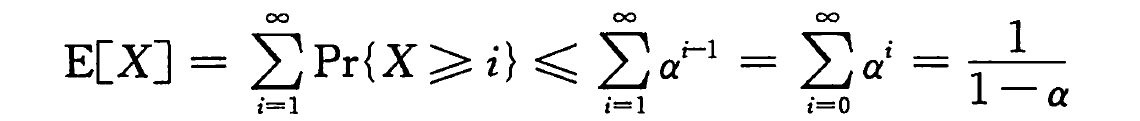
对于一个装载因子为 α < 1 的开放寻址散列表，假设采用均匀散列，且表中的每个关键字被查找的可能性是相同的，一次成功查找中的探查期望数至多为 1/α · ln(1/(1-α)) 。

证明：

查找操作中所遍历的位置序列，与插入该关键字 k 时所遍历的位置序列是相同的。

假设 k 是第 i+1 个插入的关键字，则由上一定理，k 的探查的期望次数至多为 m/(m-i) 。

对散列表中所有 n 个关键字求平均，则得到一次成功查找的探查期望次数为：

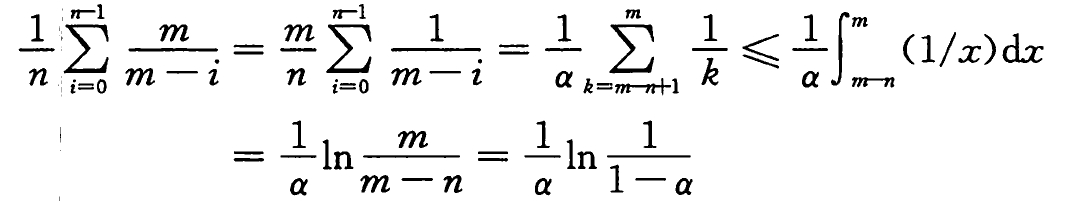
哈希函数

哈希函数将关键字所组成的域到散列表索引所组成的域。

一个好的哈希函数应（近似地）满足简单均匀散列假设：每个关键字都被等可能地散列 m 个槽位中的任何一个，并与其他关键字已散列到哪个槽位无关。

此外，哈希函数的某些情况可能会要求比简单均匀散列更强的性质。例如，可能希望某些很近似的关键字具有截然不同的散列值。

除法散列法

通过取 k 除以 m 的余数，将关键字 k 映射到 m 个槽中的某一个上。

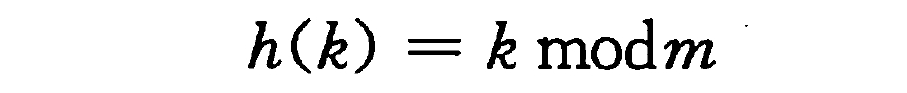
当应用除法散列法时，要避免选择 m 的某些值。例如，m 不应为 2 的幂，因为如果 m=2p，则 h(k) 就是 k 的 p 个最低位数字。

一个不太接近 2 的整数幂的素数，常常是 m 的一个较好的选择。

乘法散列法

乘法散列法分两步：

  • 用关键字 k 乘上常数 A (0<A<1)，并提取 kA 的小数部分。

  • 用 m 乘以这个值，再向下取整。

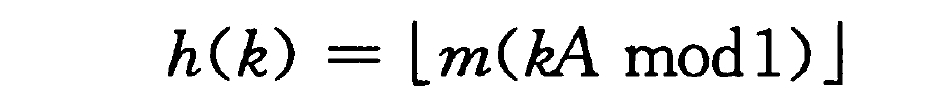
乘法散列法的一个优点是：对 m 的选择不是特别关键，一般选择它为 2 的某个幂次(m=2p, p为某个整数）。这是因为如此在计算机上容易表示。

虽然这个方法对任何的A 值都适用，但对某些值效果更好（如：黄金分割比例倒数）。

全域散列法

一般情况下，哈希函数能将随机的输入均匀的映射到散列表的各个槽中。

但是如果有人恶意针对某个固定的哈希函数，故意输入n个关键字，被哈希函数映射到同一个槽中，那么平均检索时间退化为 Θ(n) 。

为了避免这种困境，我们将随机地选择哈希函数。这种方法称为：全域散列（universal hashing）。

当然，随机选择并不是乱选，而是从一组预先设计（全域的）的函数 H 中，随机地选择一个哈希函数 h。

设 H 为一组有限的散列函数，它们将关键字全域 U 映射到 {0, 1, …, m-1} 中。如果它们对每一对不同的关键字 k，l ∈ U，满足 h(k) = h(l) 的散列函数 h ∈ H 的个数至多为 |H|/m，那么这组函数 H 称为全域的（universal）。

这表明了两点性质：

  • 如果从 H 中随机地选择一个散列函数，当关键字 k ≠ l 时，两者发生冲突的概率不大于 1/m。
  • 这也正好是从集合{0, 1, …, m-1} 中独立地随机选择 h(k) 和 h(l) 时发生冲突的概率。

我们可以证明，全域散列法能均匀地将关键字映射进各个槽中。

如果 h 选自一组全域散列函数，将 n 个关键字散列到一个大小为 m 的表 T 中，并用链接法解决冲突。

  • 如果关键字 k 不在表中，则 k 被散列到的链表的期望长度 E[nh(k)] 至多为 α = n/m。
  • 如果关键字 k 在表中，则包含关键字 k 的链表的期望长度 E[nh(k)] 至多为 **1+ α**。

证明：

由于上述的性质1，我们知道：对于每一个关键字 k，其余关键字与之冲突的概率 ≤ 1/m。所以与 k 映射到同一个槽的关键字个数的期望为：n/m = α。

  • 如果关键字 k 不在表中，则 k 被散列到的链表的期望长度至多为 α = n/m。
  • 如果关键字 k 在表中，则计数时需要算上 k，所以再 +1。

如何设计一组全域哈希函数呢？

  1. 选择一个足够大的素数 p，使得每一个可能的关键字 k 都落在 [0, p-1] 。

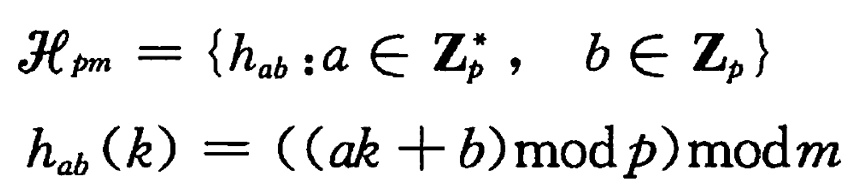
完全散列

当关键字集合是静态（static）时，散列技术也能提供出色的最坏情况性能。所谓静态，就是指一旦各关键字存入表中，关键字集合就不再变化了。

针对这一情形，我们采用：完全散列（perfect hashing）。

如果该方法进行查找时，能在最坏情况下用 O(1) 时间完成。

我们采用两级的散列方法来设计完全散列方案，在每级上都使用全域散列。

  • 第一级与链地址法相同：从一组全域哈希函数中选出一个函数 h，将 n 个关键字映射到 m 个槽中。
  • 第二级中，我们建立一个较小的散列表。
    • 通过选取合适的哈希函数 hi，保证第二级散列表上不会发生冲突。（从一组全域哈希函数中随机选，如果冲突，则随机再选，直到选出。）
    • 第二级散列表 Si 的大小 mi 总是被散列到槽中的元素个数 ni 的平方。

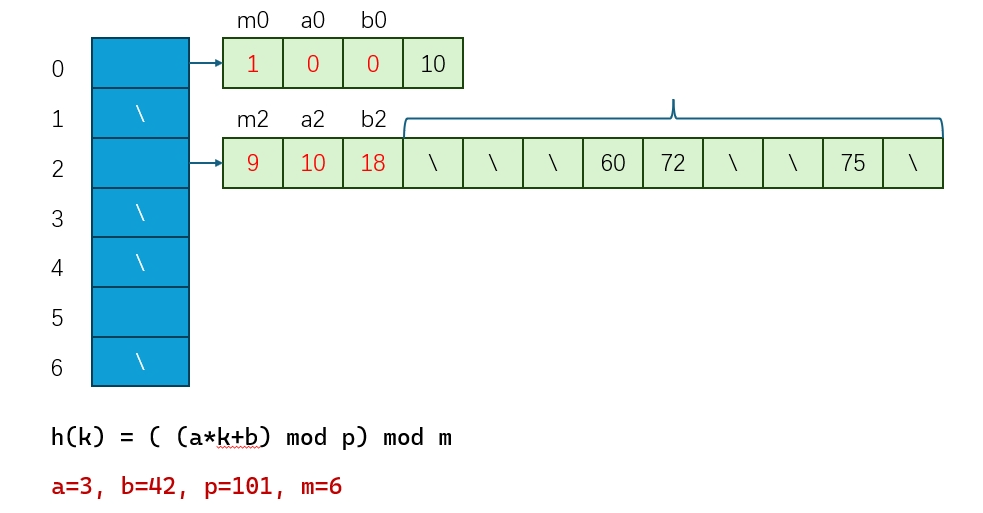
完全散列表

我们可以证明：在第二级散列表选取哈希函数时，比较容易选出一个哈希函数，不存在冲突。

如果从一个全域散列函数类中随机选出散列函数 h，将 n 个关键宇存储在一个大小为 m = n2 的散列表中，那么表中出现的冲突个数的期望小于 1/2。

此外，我们可以证明：通过合适地选取第一级哈希函数，预期使用的总空间大小为 O(n)。

image-20241105205626057

python 代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
import random
from sympy import isprime


# 全域线性哈希函数
def uni_hash(a, b, p, m, key):
    return (a * key + b) % p % m


class SubHashTable:
    """子散列表"""

    def __init__(self, sub_keys=[]):
        self.n = len(sub_keys)
        self.m = len(sub_keys) ** 2

        # 获取大于maxVal的最小素数
        maxVal = max(sub_keys) if len(sub_keys) != 0 else 0
        maxVal = max(maxVal, self.m)
        self.p = maxVal + maxVal % 2 + 1
        while not isprime(self.p):
            self.p += 2

        # 填充键值, 保证不冲突
        is_conflict = True
        while is_conflict:
            is_conflict = False
            self.nums = [None] * self.m
            self.a = random.randint(1, self.p - 1)
            self.b = random.randint(0, self.p - 1)

            # 遍历子键, 填充哈希表
            for key in sub_keys:
                idx = uni_hash(self.a, self.b, self.p, self.m, key)
                if self.nums[idx] is not None:
                    is_conflict = True
                    break
                self.nums[idx] = key

    # 插入键值, 并重建哈希表
    def insert(self, key):
        if self.search(key):
            return
        subkeys = [k for k in self.nums if k is not None]
        subkeys.append(key)
        self.__init__(subkeys)

    # 删除键值, 并重建哈希表
    def delete(self, key):
        subkeys = [k for k in self.nums if k is not None and k != key]
        self.__init__(subkeys)

    def search(self, key):
        if self.n == 0:
            return False
        idx = uni_hash(self.a, self.b, self.p, self.m, key)
        return self.nums[idx] == key


class PerfectHashTable:
    """完全散列"""

    def __init__(self, m=10):
        self.m = m
        self.sub_table = [SubHashTable()] * m

    def insert(self, key):
        idx = key % self.m
        self.sub_table[idx].insert(key)

    def delete(self, key):
        idx = key % self.m
        self.sub_table[idx].delete(key)

    def search(self, key):
        idx = key % self.m
        return self.sub_table[idx].search(key)


# 测试功能是否有效
if __name__ == "__main__":
    pht = PerfectHashTable()
    ref_set = set()
    for _ in range(100):
        key = random.randint(0, 10000)
        ref_set.add(key)
        pht.insert(key)

    for key in ref_set:
        assert pht.search(key) == True
        pht.delete(key)
        assert pht.search(key) == False
    print("All tests passed.")