延绪的水上书
0%

快速排序

发表于 更新于 分类于 Disqus：

快速排序

快速排序也是一种分治算法。

快速排序分为三步：

  1. 分解：数组 A[p.. r] 被划分为两个（可能为空）子数组 A[p.. q-1] 和 A[q+ 1.. r]。
    • A[p .. q-1] 中的每一个元素都小于等于 A[q]。
    • A[q] 也小于等于 A[q+1..r] 中的每个元素。
  2. 解决：对划分出的两个子数组，分别递归调用快速排序。
  3. 合并：由于子数组都是原址排序的，所以不需要合并操作。

伪代码如下：

1
2
3
4
5
QUICKSORT(A, p, r)
	if p < r
		q = PARTITION(A, p, r)
		QUICKSORT(A, p, q-1)
		QUICKSORT(A, q+1, r)
1
2
3
4
5
6
7
8
9
PARTITION(A, p, r)
	x = A[r]
	i = p—1
	for j = p to r-1
		if A[j] <= x
			i = i + 1
			exchange A[i] with A[j]
	exchange A[i+1] with A[r]
	return i + 1

图片

快排性能

最坏情况

当划分产生的两个子问题分别包含了 n-1 个元素和 0 个元素时，快速排序的最坏情况发生了。

此时运行时间的递推公式为：

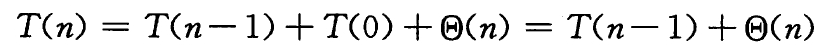
我们通过归纳法，可以证明：最坏情况下，快速排序的运行时间为 **Θ(n2)**。

此外，当输入数组已经完全有序时，快速排序的时间复杂度仍然为 **Θ(n2)**。

最好情况

在可能的最平衡的划分中，PARTITION 得到的两个子问题的规模都不大于 n/2。

此时运行时间的递推公式为：

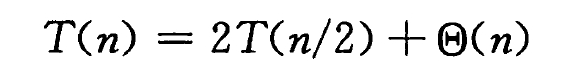
我们通过主定理，可以证明：最好情况下，快速排序的运行时间为 **Θ(n · lgn)**。

一般情况

快速排序的平均运行时间更接近于其最好情况，而非最坏情况。

我们举例说明：

例子

随机化的快排

在讨论快速排序的平均情况性能的时候，我们的前提假设是：输入数据的所有排列都是等概率出现。但在现实中，这个假设并不总是成立的。所以对于一些输入，快排的最坏情况可能经常发生。

为了避免，我们引入随机化版本：每次划分时，随机选择基准（pivot）。

伪代码如下：

快排函数：几乎没有变化，只是将划分函数 PARTITION 替换为新的 RANDOMIZED-PARTITION。

1
2
3
4
5
RANOOMIZED-QUICKSORT CA, p, r)
	if p<r
		q = RANDOMIZED-PARTITION (A, p, r)
	RANOOMIZED-QUICKSORT (A, p, q-1)
	RANOOMIZED-QUICKSORT (A, q+1, r)

划分函数：从子数组中随机选择基准

1
2
3
4
RANDOMIZED-PARTITION (A, p, r)
	i = RANDOM(p, r)
	exchange A[r] with A[i]
	return PARTITION(A, p, r)