分治策略 | 延绪的水上书

何为分治

分治算法通常用于解决递归问题，特别是在处理可以划分为相似子问题的情况下。

具体来说，分治算法分为三步（在每层递归中）：

分解（Divide）：将问题划分为一些子问题，子问题的形式与原问题一样，只是规模更小。
解决（Conquer）：递归地求解出子问题。如果子问题的规模足够小，则停止递归，直接求解。
合并（Combine）：将子问题的解组合成原问题的解。

递归式

当我们计算分治算法的运行时间，自然地会使用递归公式来刻画。

所以如何求解递归式（求出算法运行时间的 Θ 或 O 渐近界）是很重要的。这里介绍三种方法：

代入法：先猜后证，数学归纳。
递归树法：画树状图。
主方法：求解形如T(n) = aT(n/b) + f(n)的递归式。

代入法

代入法很朴素，就两步：

猜测解的形式。
用数学归纳法证明：解是对的。

例题：

T(n) = 2T(n/2) + n

题解：

我们猜测 T(n) = O(n·lgn)
即欲证：T(n) <= c·n·lgn, ∃c > 0

归纳假设：T(n/2) <= c(n/2)·lg(n/2), ∃c > 0
那么：
T(n) <= 2(c·n/2·lg(n/2)) + n
	 = c·n·lgn - c·n + n
	 <= c·n·lgn
	 当 c >= 1 时

综上，T(n) = O(n·lgn)。

实际上，我们可以证明：T(n) = Θ(n·lgn)。

递归树法

虽然代入法可以简洁地证明一个解确是递归式的正确解，但做出一个好的猜测可能会很困难。画递归树则适合用来生成好的猜测。

在递归树中，我们将递归式转换为一棵树：

每个结点表示一个单一子问题的代价，子问题对应某次递归函数调用。
我们将树中每层中的代价求和，得到每层代价。
然后将所有层的代价求和，得到所有层次的递归调用的总代价。

例题：

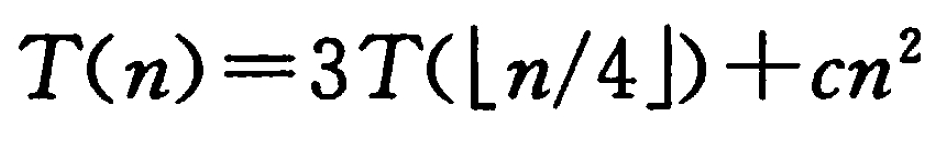
题解：

我们一层层展开递归树：

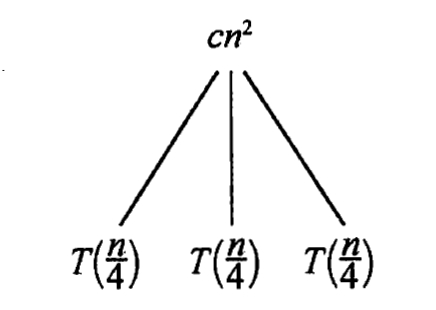
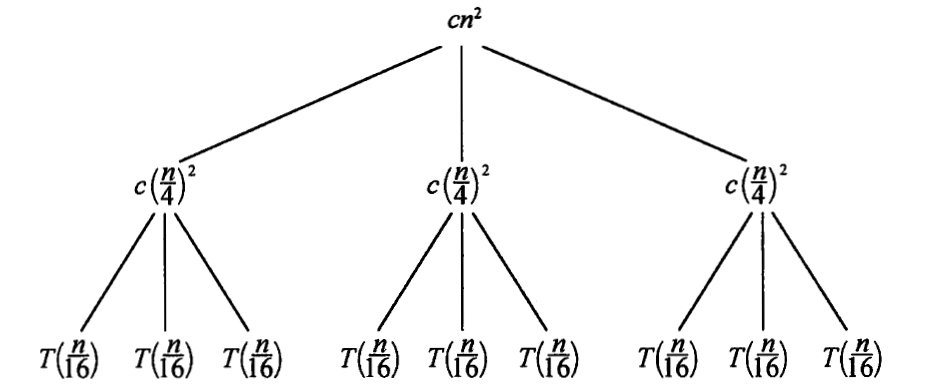
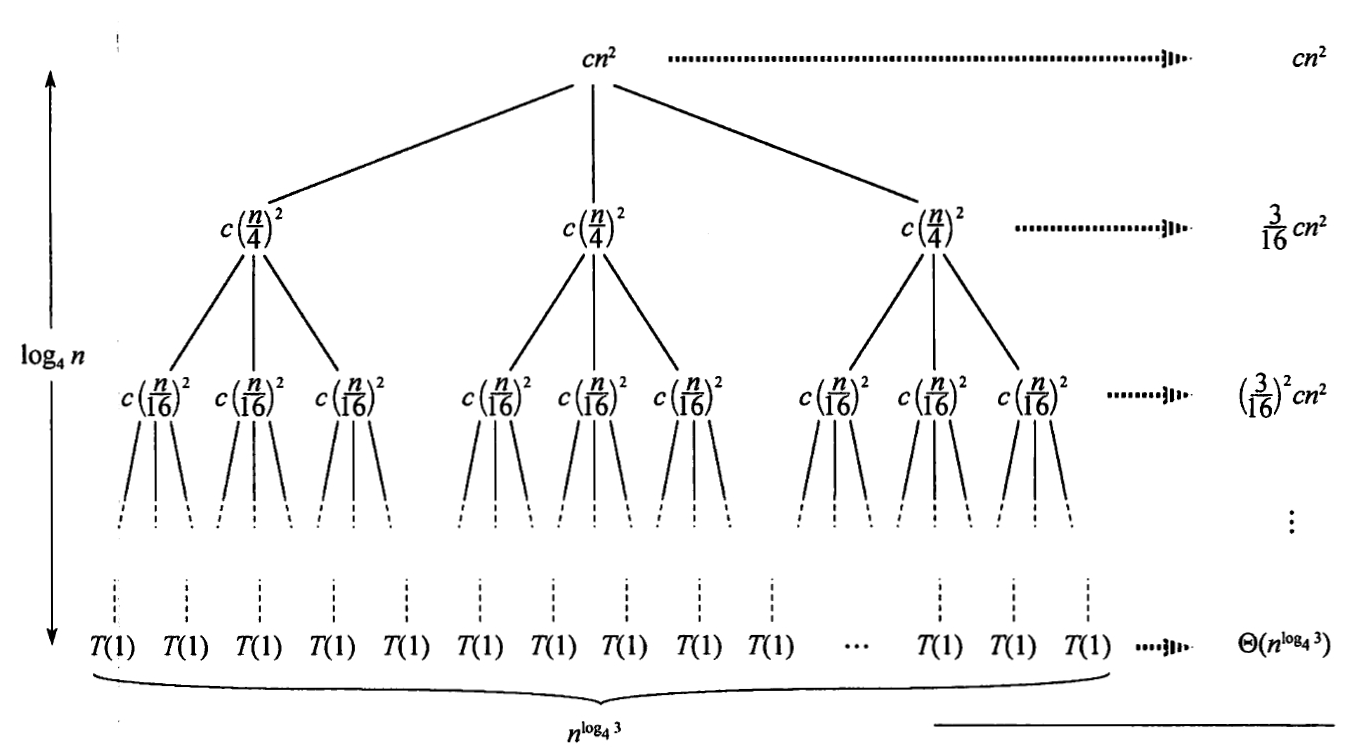
则我们的时间总开销为：

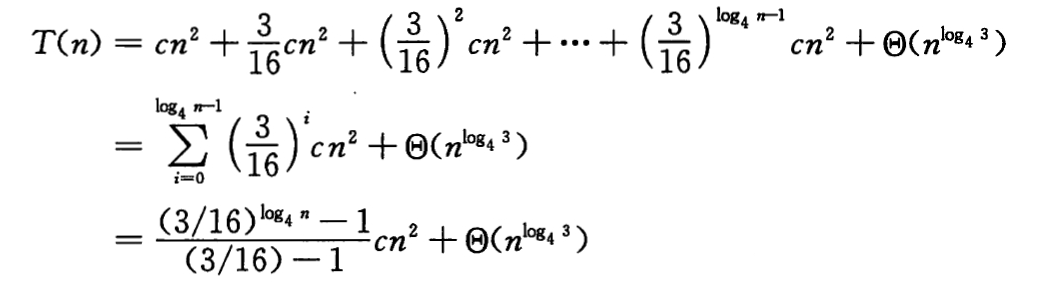
综上：T(n) 是 n 平方量级的。

主方法

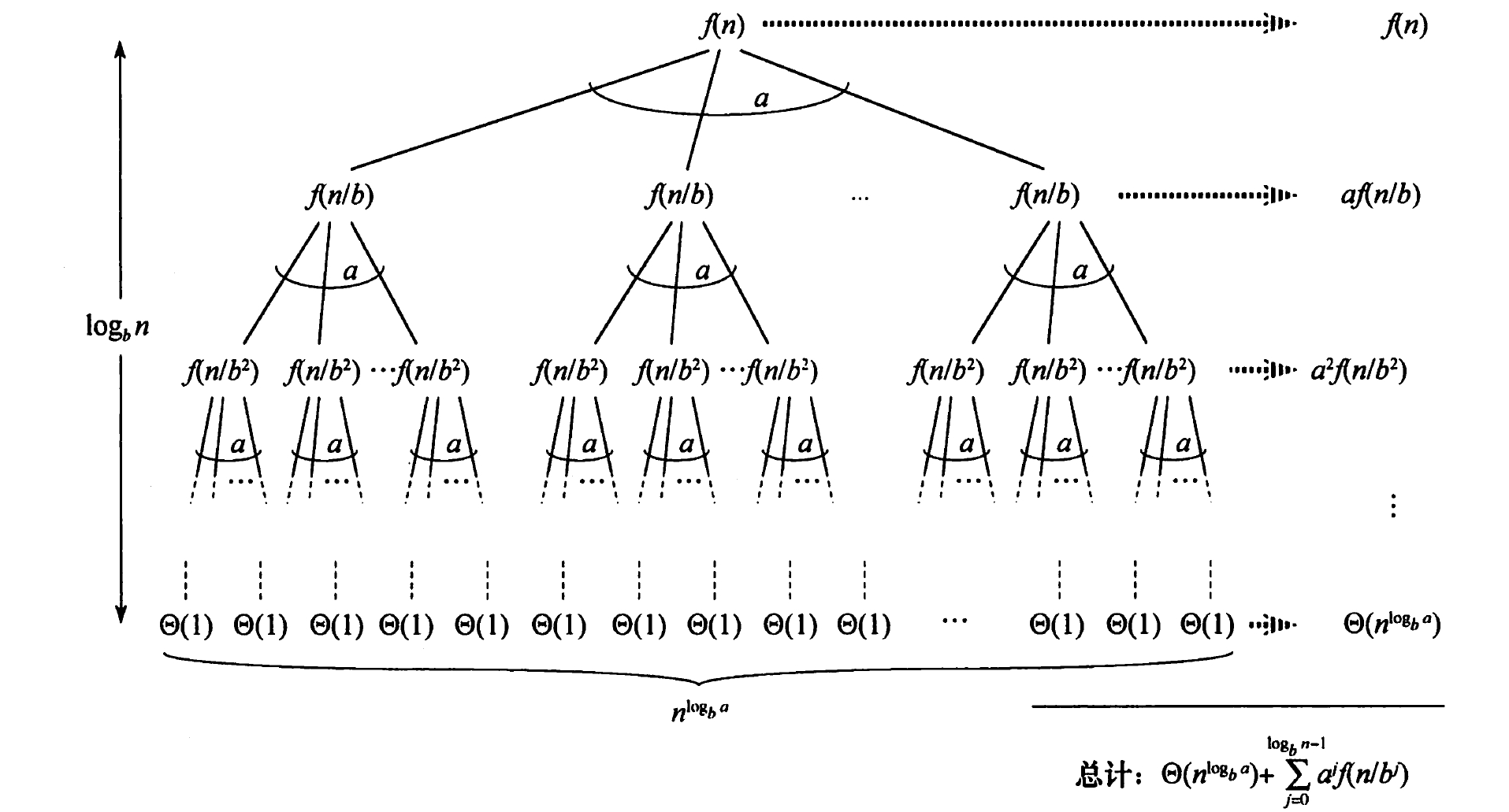
对于一些常见且特别的递归式，我们给出主定理。

主定理的证明，核心是：画递归树、分类讨论。

实例

归并排序 Vs 快速排序

归并排序和快速排序本质上都是分治算法。递推公式均是：T(n) = 2·T(n/2) + O(n)。

	Divide	Conquer	Combine
归并排序	O(1)	2·T(n/2)	O(n)
快速排序	O(n)	2·T(n/2)	0

根据主方法，我们可以知道，两者的渐近时间复杂度都是**O(n·lgn)**，都是很高效的排序方法。

但两者还是有细微的区别：

快速排序实际执行的快慢是随机的，很大程度上受pivot的影响。

最好情况是 pivot 恰好是当前子列的中位数。

最坏情况是 pivot 是最大或者最小值，则经历一次划分，几乎没有对换，也即是：花费O(n)时间却只排好了一个元素。
在数据规模不大的时候，归并排序不一定很快。这是因为：归并排序有大量递归，函数栈很深，且每次调用函数都有额外开销。

归并排序（Merge Sort）

# 归并排序步骤：
# 1.Divide: Trivial.
# 2.Conquer: Recursively sort 2 subarrays.
# 3.Combine: Linear-time merge.
# 所以：T(n) = 2·T(n/2) + O(n)

def merge_sort(arr):
    if len(arr) > 1:
        # 找到中间位置，将数组分成两半
        mid = len(arr) // 2
        # 分别对两半进行归并排序
        left_half = merge_sort(arr[:mid])
        right_half = merge_sort(arr[mid:])

        # 合并两个排序好的部分，线性时间内完成（merge函数省略了）
        arr[:] = merge(left_half, right_half)
    return arr

快速排序（Quick Sort）

# 快速排序步骤：
# 1.从列表中选择一个元素作为“基准”（pivot）。
# 2.重新排列列表，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（等于基准值的元素可以放到任一边）。
# 3.递归地把小于基准值元素的子列表和大于基准值元素的子列表排序。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        less = [x for x in arr[1:] if x <= pivot]
        greater = [x for x in arr[1:] if x > pivot]
        return quick_sort(less) + [pivot] + quick_sort(greater)

斐波那契数列

求斐波那契数列第n项是一个非常经典的分治问题，但却有很多种不同的分治策略。

算法1：自底向上

从数列的第一项开始，一项项递推。（这也是简单的动态规划算法）

不难看出，该算法的时间复杂度是：O(n) 。

# python代码实现
def fibonacci_dp(n):
    if n <= 0:
        return 0
    dp = [0] * (n + 1)
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

算法2：矩阵快速幂

首先，我们注意到斐波那契数列如下的性质。

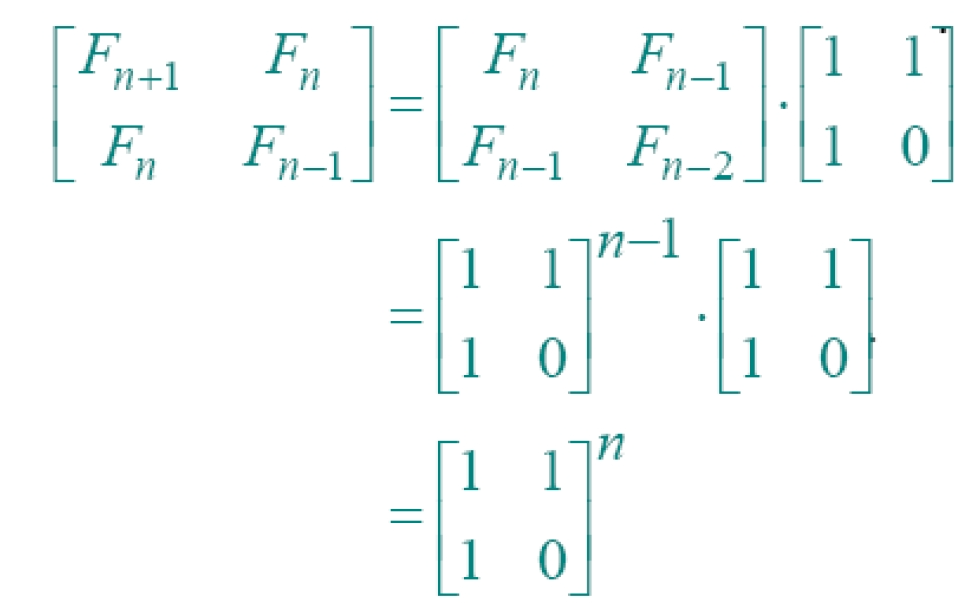
所以，“求解数列第n项”转换成：如何快速的求矩阵的幂次。

如何求幂次呢？最简单的方法是：循环n次，累乘。但这显然不是最快速的。

最快速的方法是二分算法：将 n 次幂拆分成求解 [n/2] 次幂的平方，以此类推。此时的时间开销为：**O(lgn)**。

算法3：通项公式

常言道：“暴力出奇迹”。我们可以直接计算通项公式，结果为float型，再取整即可。

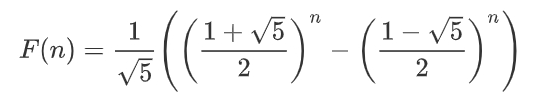
# python代码实现
import math

def fibonacci_binet(n):
    phi = (1 + math.sqrt(5)) / 2
    psi = (1 - math.sqrt(5)) / 2
    return round((phi**n - psi**n) / math.sqrt(5))

矩阵乘法

计算机大量的计算是矩阵乘法。如何高效的完成两个矩阵的乘法呢？

算法1：三重循环

根据矩阵乘法的定义，我们可以在 O(n³) 内完成。

伪代码如下：

function MATRIX_MULTIPLY(A, B):
    # 三重循环，执行矩阵乘法
    for i = 1 to n:                  # 遍历A的每一行
        for j = 1 to n:              # 遍历B的每一列
            for k = 1 to n:
                C[i][j] = C[i][j] + A[i][k] * B[k][j]
    return C

算法2：分块矩阵

简单起见，我们将 n 阶矩阵划分为4个 n/2 阶矩阵，以此递归。

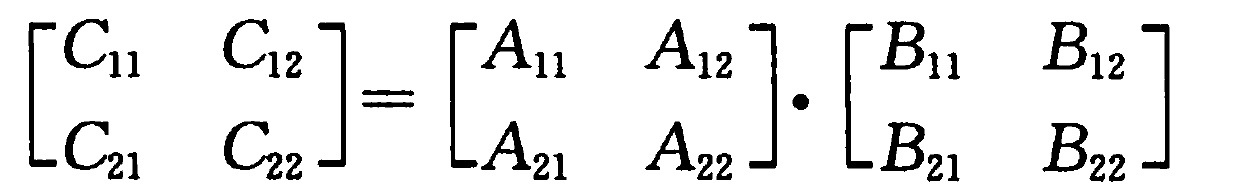
则我们每次递归需要的时间开销：

划分分块矩阵
递归计算A、B的8个子矩阵乘积
求和得到C₁₁、C₁₂、C₂₁、C₂₂。

	Divide	Conquer	Combine
T(n)	O(1)	8·T(n/2)	4·( n/2 )² = O(n²)

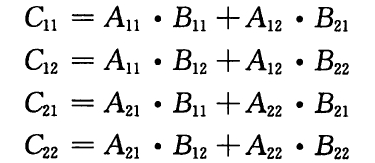
但非常遗憾，根据主方法，如此二分算法的时间开销仍是：**O(n³)**。

如何更快速呢？

核心在于：每次递归时，计算尽可能少的矩阵乘法，再通过加法组合出我们想要的子矩阵。（因为：矩阵乘法是 O(n³)，而矩阵加法是 O(n²)。）

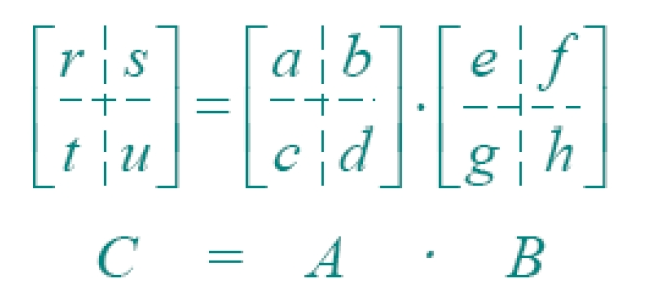
对此，我们如下改进：

我们只计算如下7个矩阵乘法。

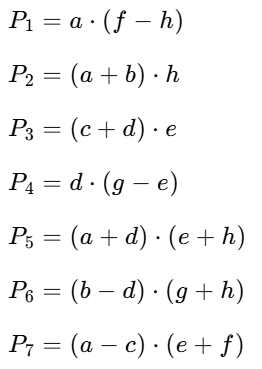
再通过加法，算出C矩阵。

r = P₅ + P₄ − P₂ + P₆
s = P₁ + P₂
t = P₃ + P₄
u = P₅ + P₁ − P₃ − P₇

此时算法的时间开销是：**O(n^log₂7)**。