引言
就像查字典有拼音索引、部首索引、笔画索引一样,为了方便查询,数据库中也有索引。主要有以下两种索引:
- 顺序索引(Ordered indices)
- 哈希索引(Hash indices)
首先,我们介绍一些预备知识。
查询记录时,我们会根据一个属性或者多个属性进行搜索。这个属性集,我们称为:搜索码(search key)。
索引包含若干索引项。索引项(index entry)由一个搜索码值和指向记录的一个或多个指针构成。
考虑到:数据库中更新记录,可以等价为先删除旧记录,在插入新记录。所以,我们只需要考虑插入索引和删除索引即可。
顺序索引
在顺序索引中,索引项是按照 search key 进行排序存储的。
但是数据的存储顺序不一定与索引项的排序顺序相同。所以,根据是否与数据的排序顺序相符合,我们将索引分为两类:
主索引( Clustering Index):索引顺序与数据顺序相同。
辅助索引(Non-clustering Index):索引顺序与数据顺序不同。
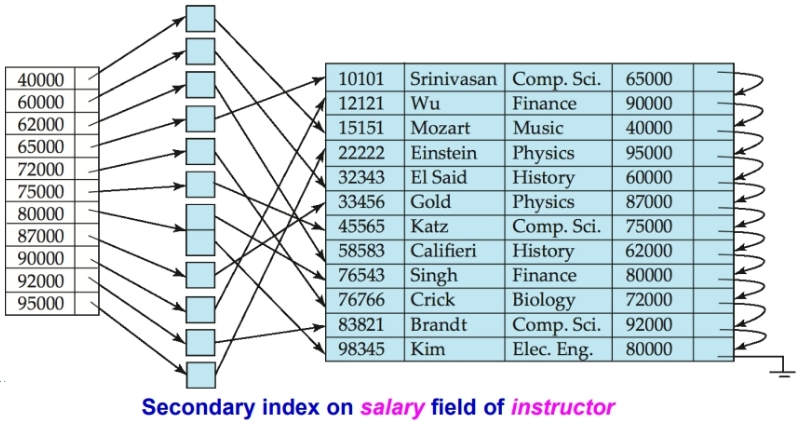
除了这种分类方式,还可以根据索引项的密度进行分类:
稠密索引(Dense Index):每一个搜索码都对应地有一个索引项。
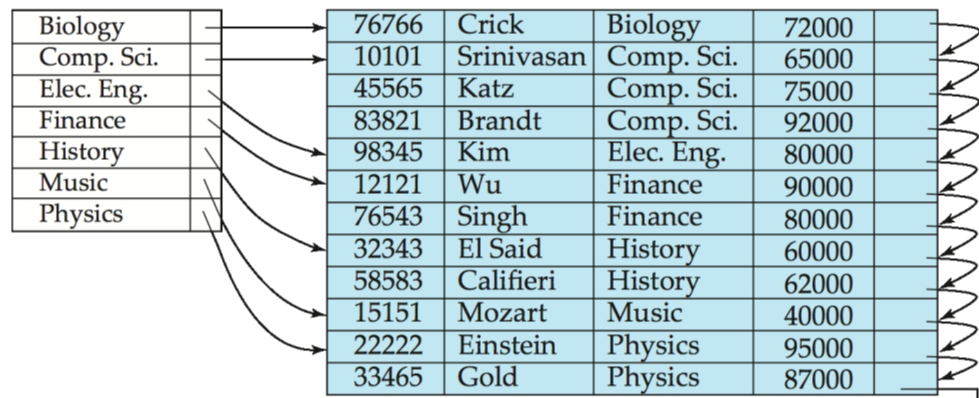
稀疏索引(Sparse Index):索引项只涵盖了部分搜索码的可能取值。
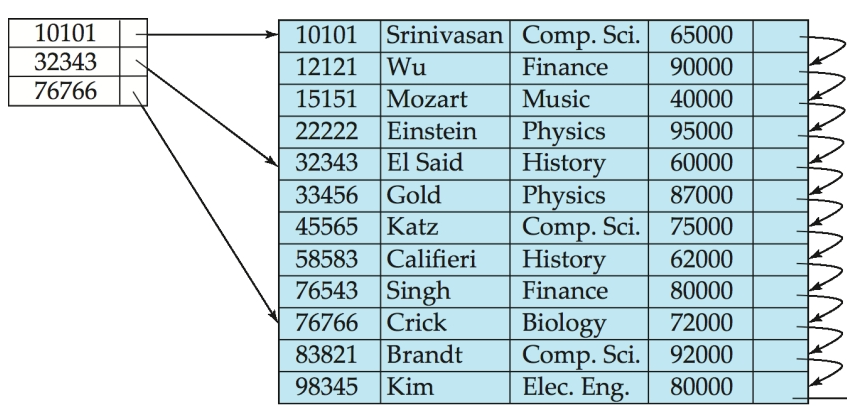
请注意:辅助索引必须是稠密索引,即每个搜索码都有一个索引项。这是因为:辅助索引的顺序与数据顺序不同,如果一个搜索码没有对应的索引项,那么这个记录可能出现在数据库中的任何地方,那么索引也就失去作用了。
显然,如果索引是聚集且稀疏的,查询一个记录则可以这么做:先在索引中寻找不大于当前搜索码值的最大索引,在从这个索引项指向的记录开始,依次往后搜索。
所以,稀疏索引的好处时可以使用更少的空间来存储索引,但定位一个记录的时间会更慢一点。所以一个不错的权衡是:生成一个稀疏索引,为每一个块建一个索引项(generate a sparse index with an index entry for every block in file)。
B+树索引
优缺点
B+树索引的好处和缺点如下:
| 优点 | 缺点 |
|---|---|
| 每次插入删除会自动重组索引结构 | 每次插入删除都有额外的时间开销 |
| 不需要重组整个文件来维持性能 | 维持B+树的空间开销 |
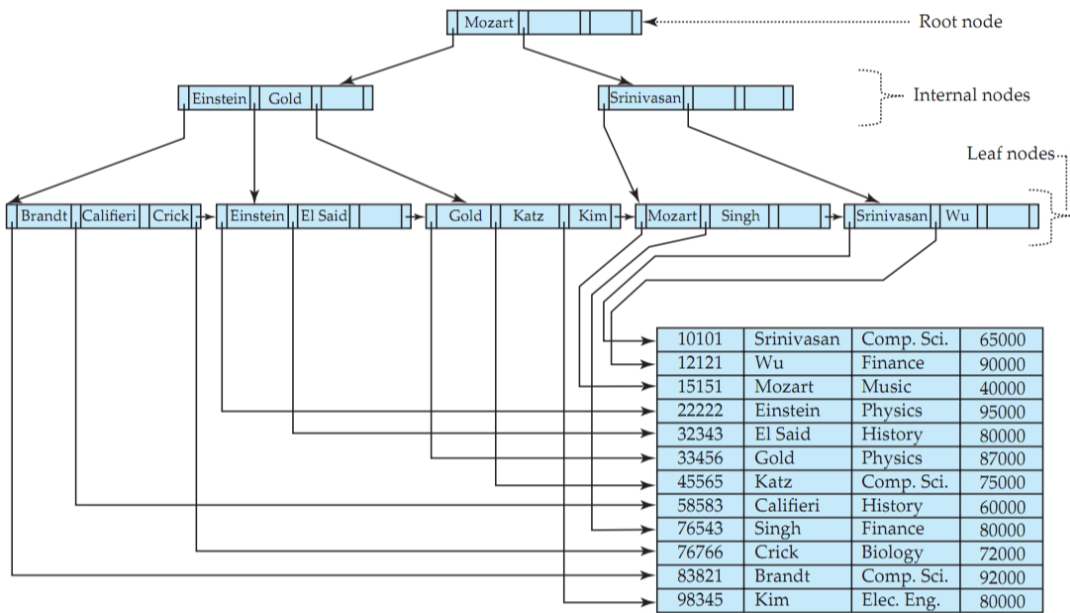
整体结构
中间节点(internal nodes):既不是根节点,也不是叶节点
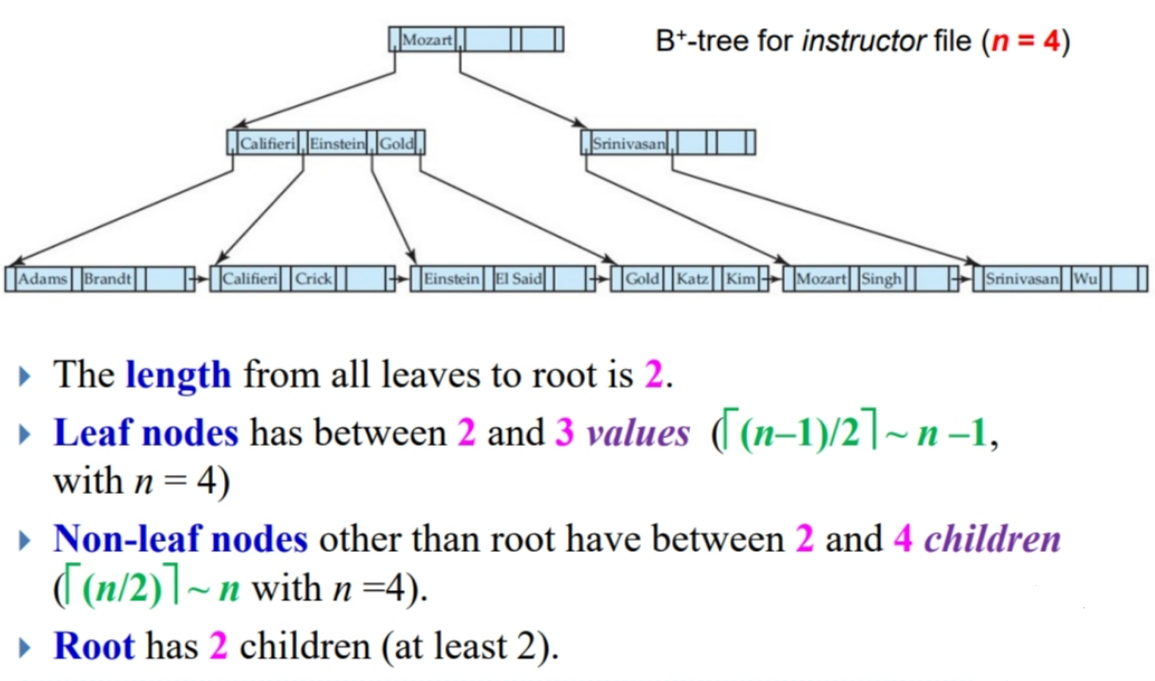
B+树是一个有根节点的树,且满足以下性质:
- 所有从根节点到叶节点的路径都一样长。(平衡树)
- 每个中间节点有 ⌈n/2⌉ 到 n 个子节点。(n预先给定的)
- 叶节点有 ⌈(n-1)/2⌉ 到 n-1个值。
- 如果根节点不是叶节点,则根节点至少有两个子节点。
- 如果根节点是叶节点,则根节点有 0 到 (n-1) 个值。
节点结构
对于非叶子节点:

其中:
指针个数 n 称为:扇出(fanout)。
**K1 < K2 < …… < Kn-1**(假设搜索码不会重复)

如果是叶子节点,则还有如下性质:
- 最后一个指针 Pn 指向下一个叶子节点。
- Pi 指向的记录的搜索码取值为 Ki 。
- 如果叶节点 Li < Lj ,那么叶节点 Li 中所有记录的搜索码都小于等于 Lj 中的。
如果搜索码可能重复,那么 Ki 序列不再是严格单增的。而是:K1 <= K2 <= …… <= Kn-1
查询
在 B+ 树种查找搜索码为 V 的记录,方法如下(伪代码表示):
1 | set C = root node |
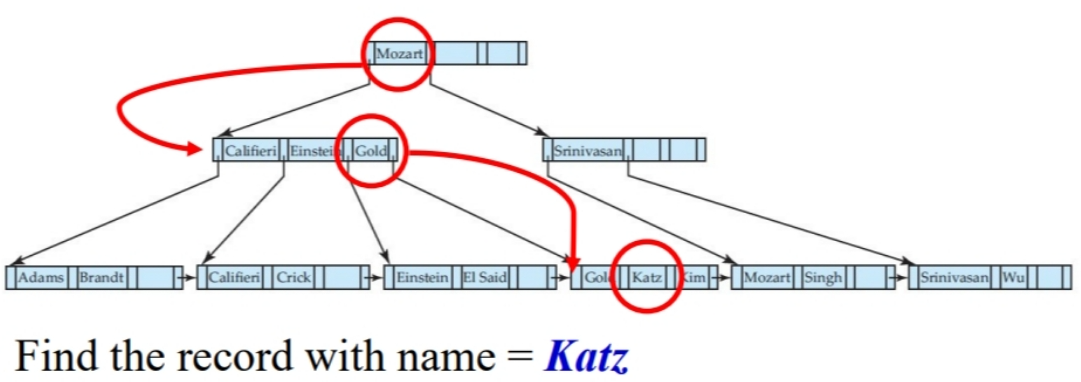
更新
由于 B+ 树对每个节点的子节点数有限制,所以每次插入删除都可能需要:
- Split a node if the node becomes too large.
- Coalesce (合并) two or more nodes if a node becomes too small.
分裂和合并的规则描述起来比较复杂,我们直接看例子。
插入”Adam”:
先根据之前的查询的流程来定位。
插入“Adam”,检查是否需要分裂。若需要,则分裂。
子节点分裂可能导致父节点也需要分裂,所以需要一层层向上检查。
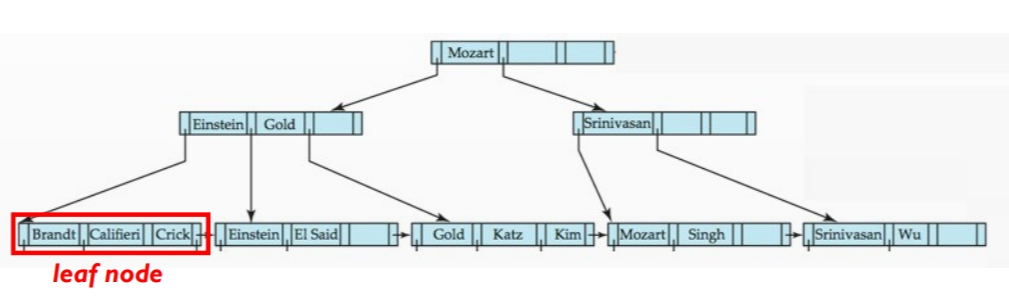
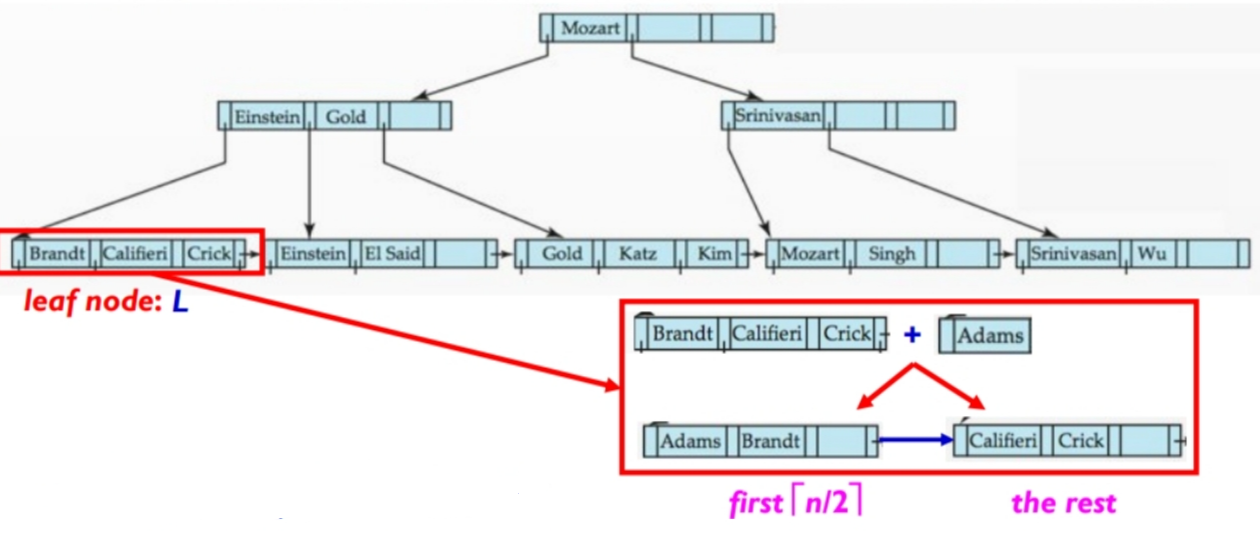
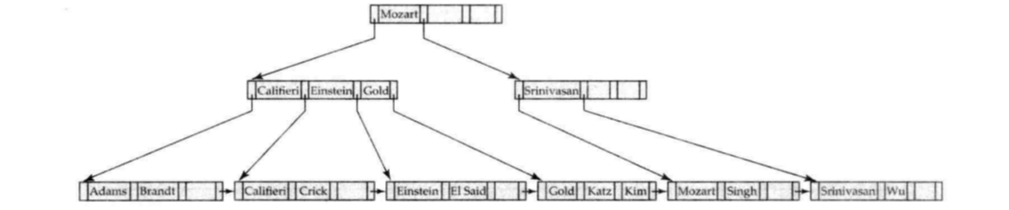
在1的基础上,再插入“Lamport”:
- 与之前类似,不过这次插入导致上层节点也需要分裂。
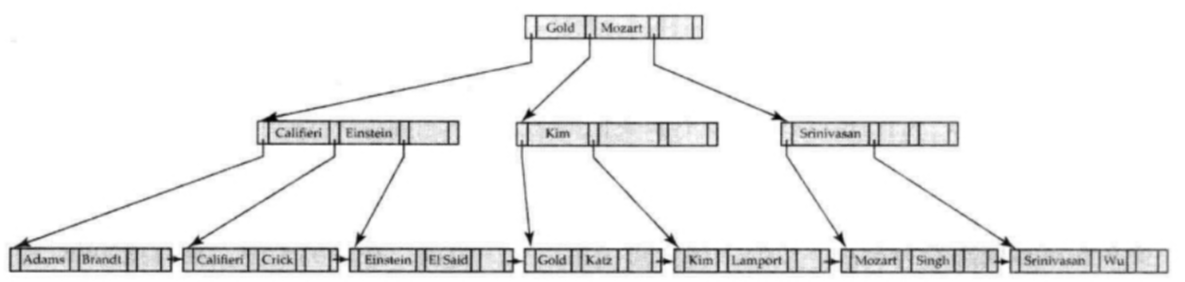
删除“Srinivasan”:
- 删除目标节点。
- 如果删除后子节点数不符合要求,那么与兄弟节点进行合并。
- 合并后,父节点可能也需要合并,所以需要向上一层层检查。
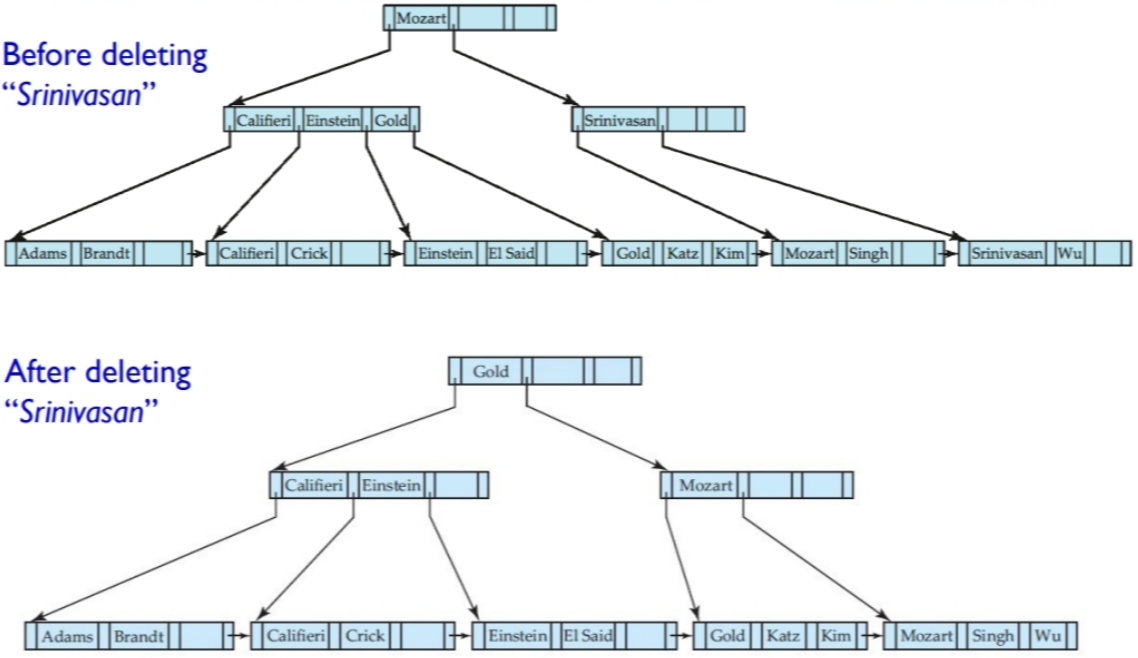
再删除“Singh”和“Wu”:
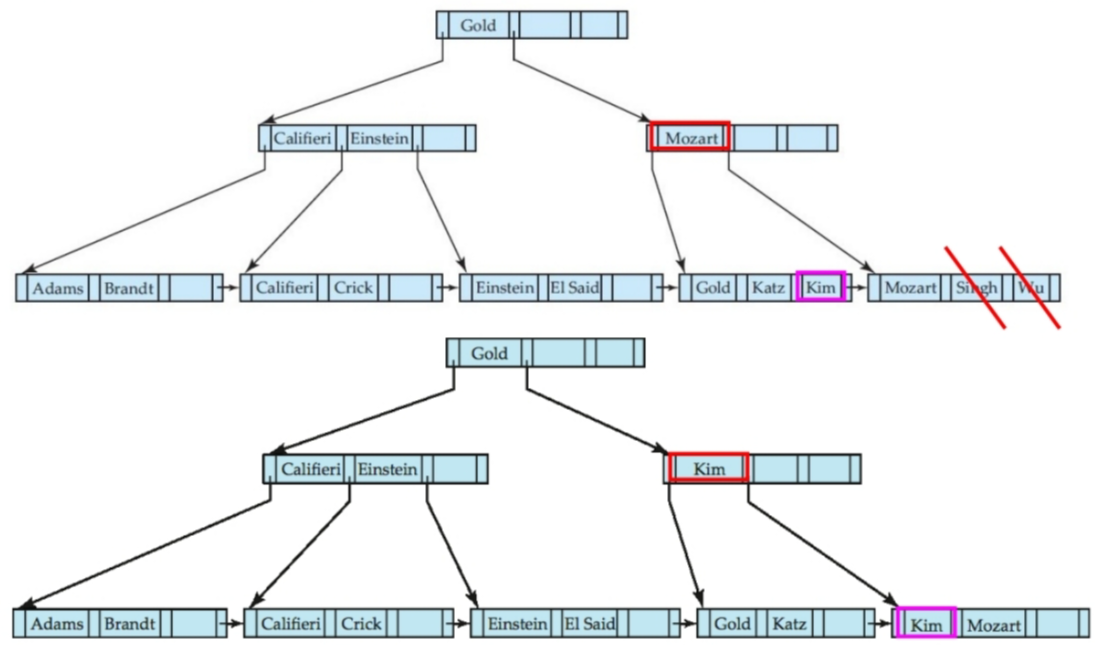
再删除“Gold”:
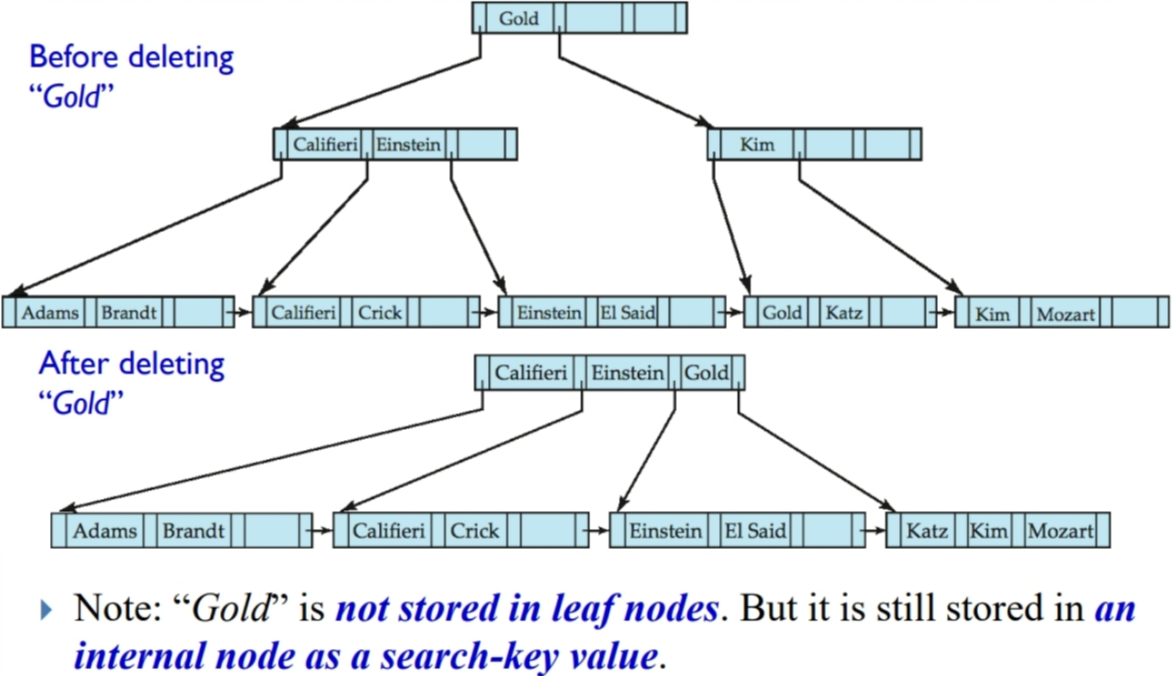
B 树索引
B 树类似于 B+ 树。B 树要求:每个搜索码的取值只能出现一次,从而消除重复储存搜索码的值。
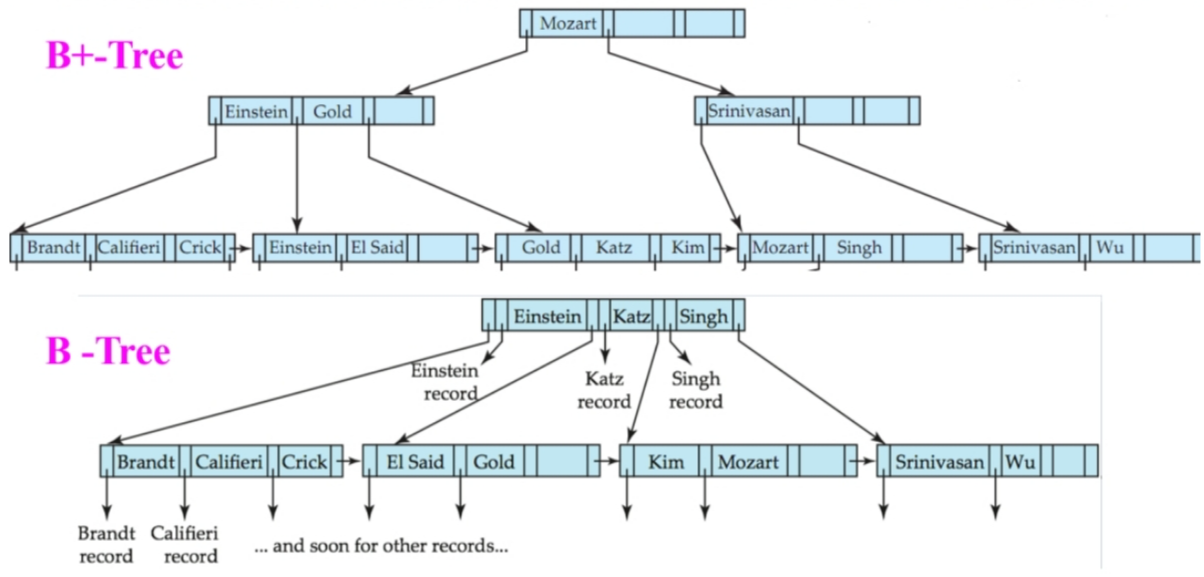
B 树优点在于:
- 使用了更少的节点
- 可能更快地找到搜索码的值(因为不一定要遍历到叶节点)
B 树缺点在于:
- 只有很小一部分的搜索码的值是可以更快找到的。
- 插入和删除操作都会更复杂
- 实现也更加麻烦
总的来说,B树不如B+树,缺点远胜优点。
哈希索引
之前的索引方式都需要建立一种索引结构,但哈希索引则可以避免:
- 通过计算哈希函数(hash function),可以由 search key 计算得到包含目标记录的块地址。
- A bucket is a unit of storage containing one or more records typically a disk block.
静态哈希
在静态哈希种,桶的数量是固定的。
常见的哈希函数都是:计算搜索码的二进制表示,再模上桶的数量。
例如下图中:根据dept_name,在instructor表上建立哈希索引。
桶个数=8。
哈希函数是:将各字母在字母表中的序号相加,再 mod 8。
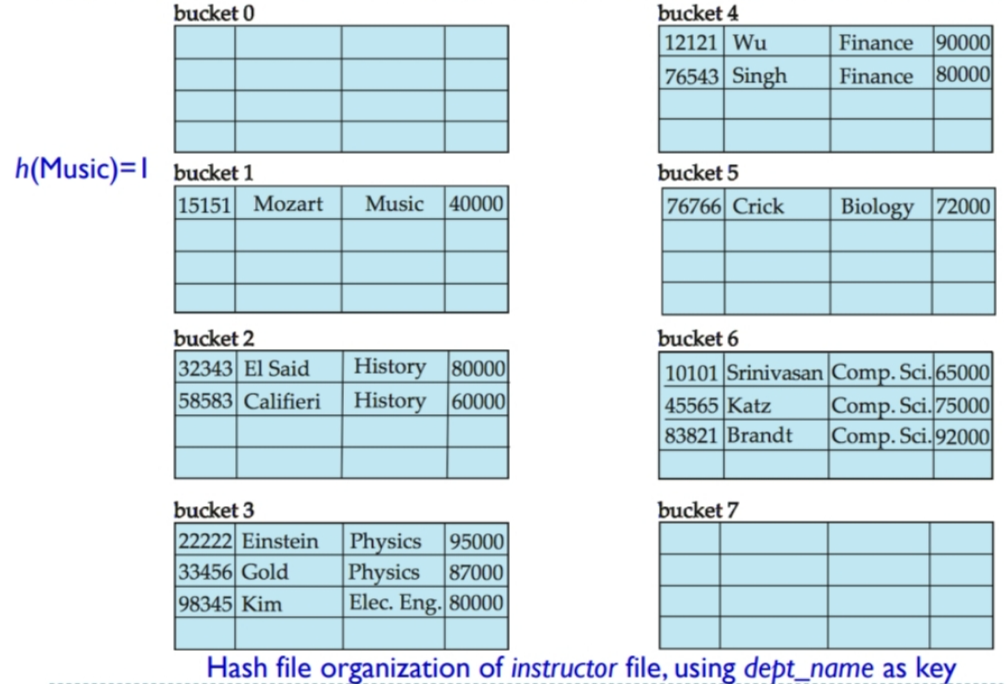
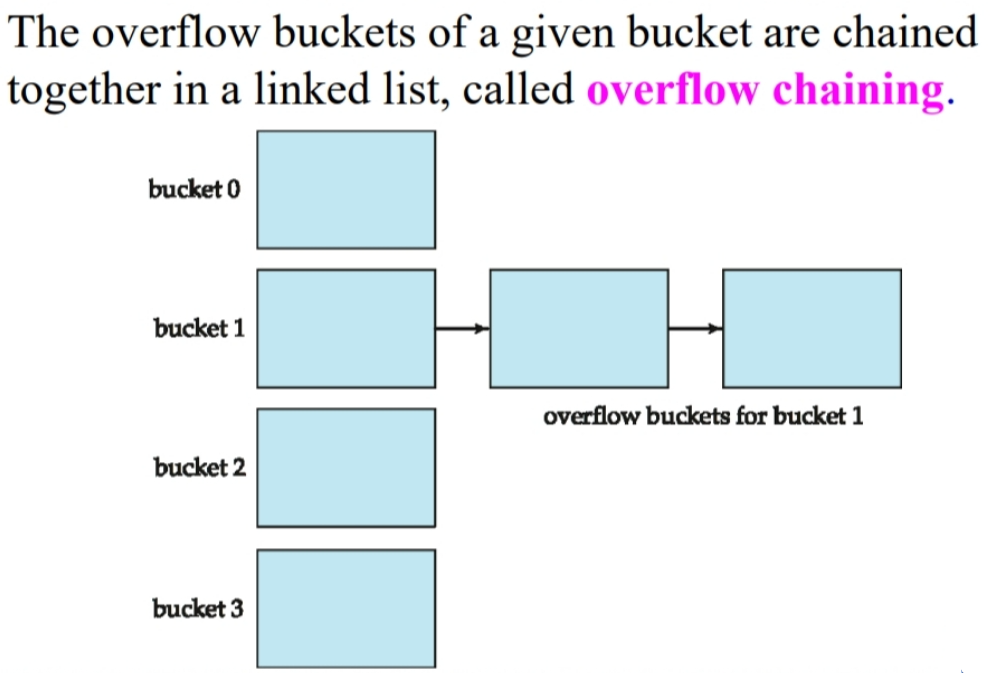
溢出桶
但如果插入记录时,发现桶里已经装满了记录,这就是:桶溢出(Bucket Overflow)。一般有如下两种原因:
- 桶确实不足。即使所有桶全部装满,也装不完全部记录。
- 很多记录都装进了同一个桶,而其他很多桶还有很多空间。(Skew in distribution of records)
解决办法也很朴素:加桶(谁溢出,谁加桶)。
动态哈希
静态哈希虽然易于实现,但缺点也明显:桶的数量是固定。
- 如果设置的太小,那么需要不停的添加溢出桶,且一个 hash地址 中的记录也会非常多,导致查询效率降低。
- 如果设置的太大,在数据规模还没起来时,大量空间被浪费了。
所以我们希望:桶的数量能动态变化。这便是:动态哈希。
这里,我们主要介绍:可扩充散列(Extendable Hashing)。
可扩充散列的核心思想是:当存储的记录不多时,我们只使用 hash 值的前几位。当存在有桶溢出的情况时,我们再使用更多的 hash 值位数。
严格来说:
- 假定 hash 函数产生的 hash 值是 b 位。
- 设每个桶所对应的 hash 值是 i 位,(0 <= i <= b)。
- 当一条记录经过 hash 函数计算得的 hash 值的前 i 位与桶的 hash 值相同时,这条记录存储在这个桶里。
- 当这个桶溢出时,这个桶会分成两个桶。它们的 hash 值都是 i+1 位,且前 i 位继承原来桶的 hash 值,最后一位则分别时0、1。原来桶中的记录依据 hash 值分别装进新的两个桶中。
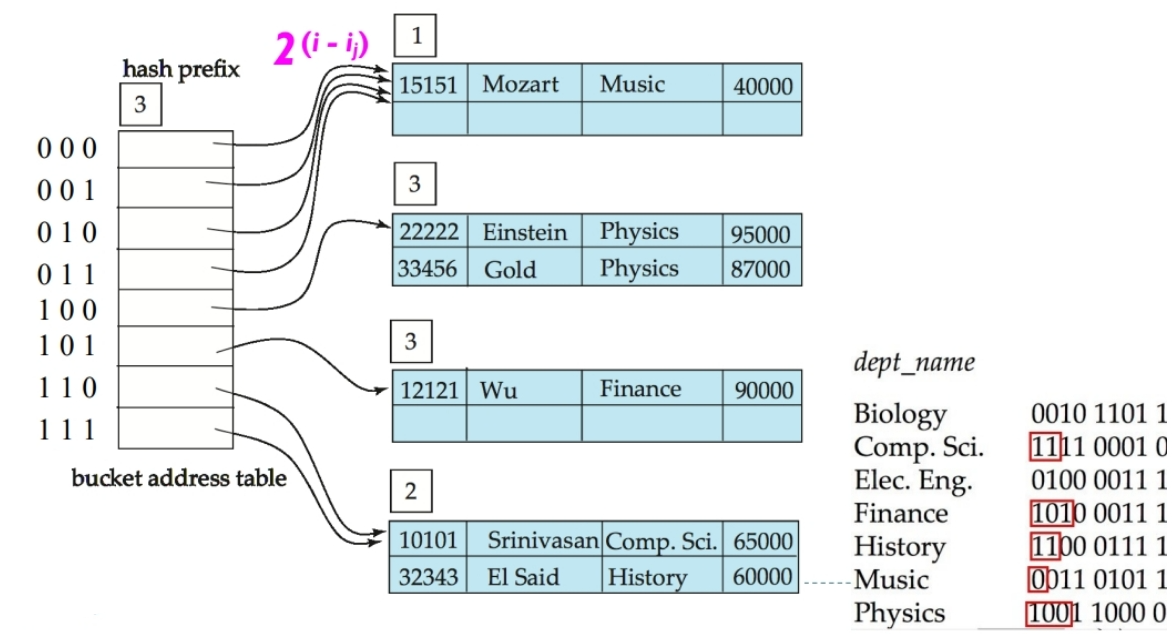
具体来说,我们举例说明:
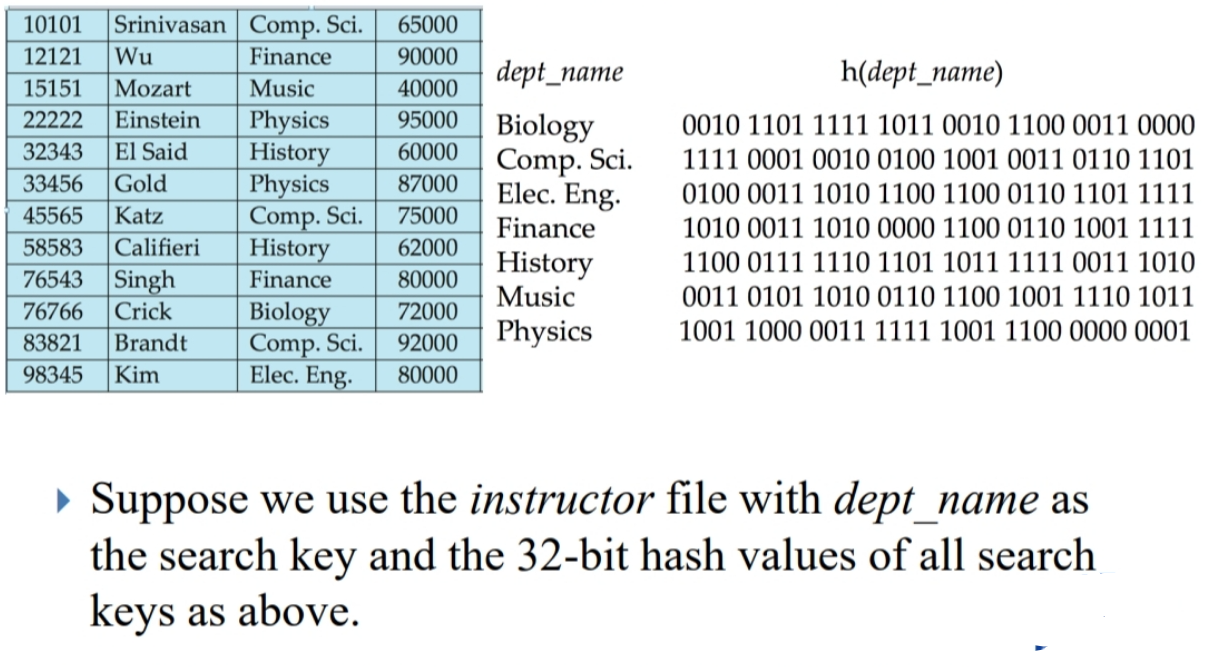
- 插入“Mozart”:
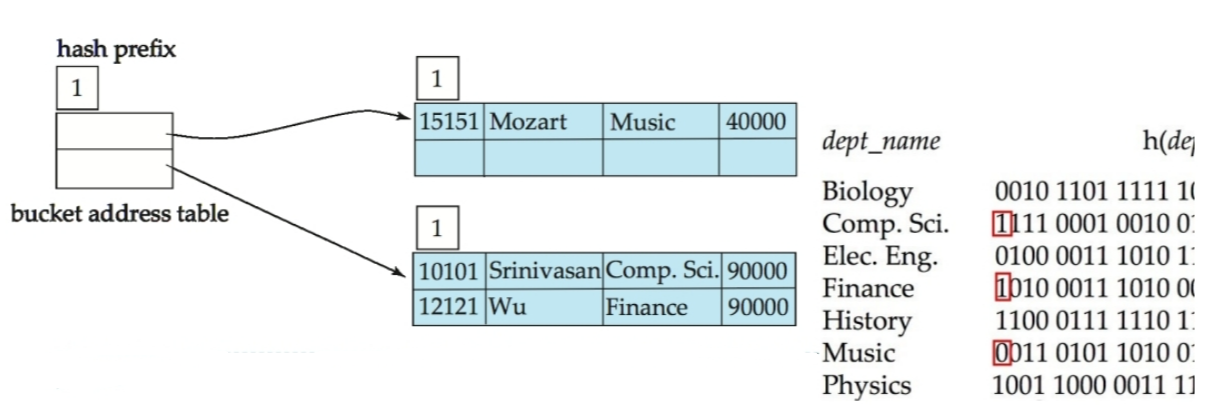
插入“Einstein”:
这时2号桶的 i2 需要加1,且 bucket address table 的前缀长度 = max { ik | k = 1, 2, … , b} 也会随着加1。
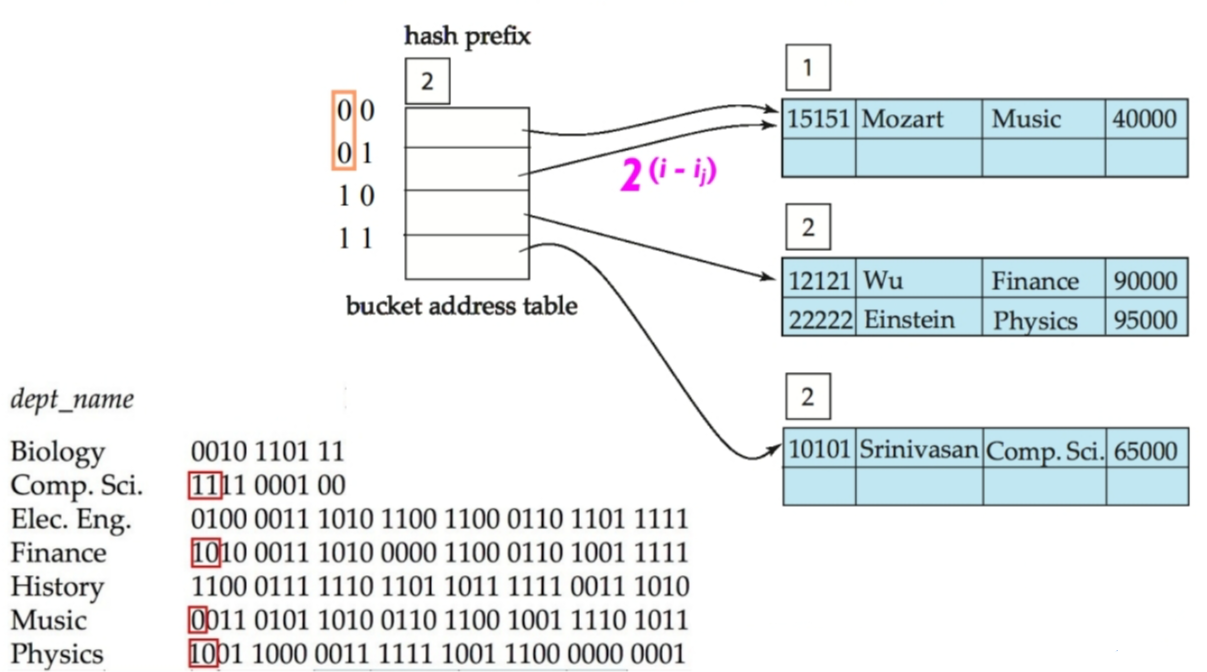
- 插入“Gold”:
一些比较
如果是范围搜索,顺序索引更好。
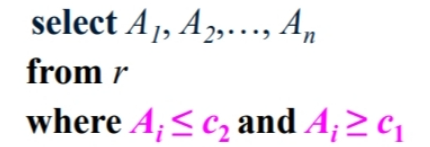
如果是搜索某个具体的值,哈希索引更好。
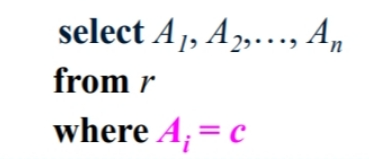
位图索引
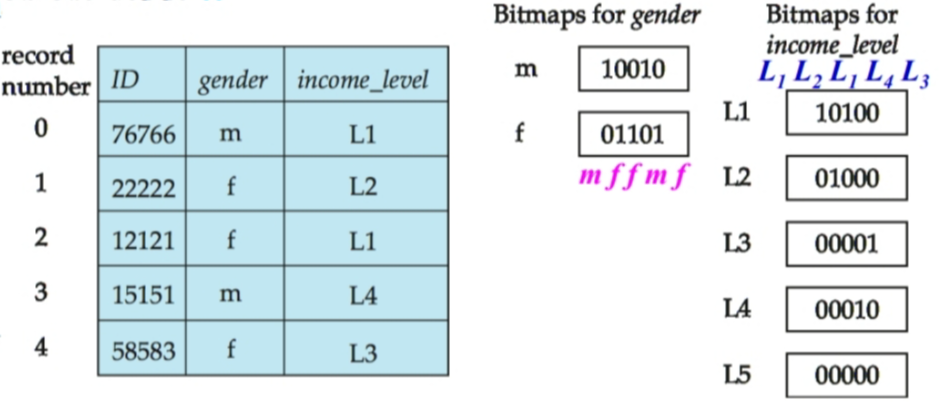
位图索引(Bitmap Index)是一种特殊但非常高效的索引。但它一般只建立一个属性上,且该属性的可能取值很少(比如:性别、国家、省)。
具体来说:
- 这个属性的每一个取值都有相应的 bitmap。
- 一个取值 V 的 bitmap 的第 i 位为1,表示第i条记录的该属性是 V。若是0,则不是 V。